ГДЗ по Математике 5 Класс Часть 2 Номер 823 Мнемозина Виленкин, Жохов — Подробные Ответы

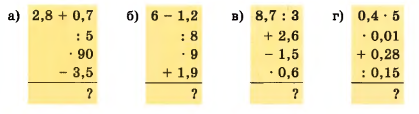
Вычислите устно:

а) \(2,8 + 0,7 = 3,5\);
\(3,5 : 5 = 0,7\);
\(0,7 \cdot 90 = 63\);
\(63 — 3,5 = 59,5\).

б) \(6 — 1,2 = 4,8\);
\(4,8 : 8 = 0,6\);
\(0,6 \cdot 9 = 5,4\);
\(5,4 + 1,9 = 7,3\).

в) \(8,7 : 3 = 2,9\);
\(2,9 + 2,6 = 5,5\);
\(5,5 — 1,5 = 4\);
\(4 \cdot 0,6 = 2,4\).

г) \(0,4 \cdot 5 = 2\);
\(2 \cdot 0,01 = 0,02\);
\(0,02 + 0,28 = 0,3\);
\(0,3 : 0,15 = 2\).

а) В первом выражении выполняется сложение чисел с десятичными дробями. Сначала складываем \(2,8\) и \(0,7\), что даёт \(3,5\). Это простая операция сложения десятичных чисел, где мы складываем целые части и дробные, учитывая запятую. Далее, чтобы найти частное от деления \(3,5\) на \(5\), делим число \(3,5\) на \(5\), получая \(0,7\). Деление десятичных чисел позволяет определить, сколько раз число \(5\) помещается в \(3,5\).

Следующий шаг — умножение \(0,7\) на \(90\). Умножение десятичных чисел на целое число позволяет увеличить исходное число в \(90\) раз, что даёт результат \(63\). В последней операции из числа \(63\) вычитаем \(3,5\), получая \(59,5\). Вычитание десятичных чисел происходит так же, как и с целыми, только с учётом десятичной части.

б) Начинаем с вычитания \(1,2\) из \(6\), что даёт \(4,8\). Важно помнить, что при вычитании десятичных дробей нужно выравнивать количество знаков после запятой. Следующим действием делим \(4,8\) на \(8\), получая \(0,6\). Деление показывает, сколько раз число \(8\) помещается в \(4,8\). Затем умножаем \(0,6\) на \(9\), что даёт \(5,4\). Умножение увеличивает число в \(9\) раз. В конце прибавляем к \(5,4\) число \(1,9\), получая \(7,3\), что является суммой двух десятичных дробей.

в) Начинаем с деления \(8,7\) на \(3\), что даёт \(2,9\). Деление десятичных чисел позволяет определить частное. Затем прибавляем к \(2,9\) число \(2,6\), получая \(5,5\). Это простое сложение десятичных дробей. Далее вычитаем из \(5,5\) число \(1,5\), получая \(4\). Вычитание уменьшает число на заданное значение. Последним действием умножаем \(4\) на \(0,6\), что даёт \(2,4\), увеличивая число в \(0,6\) раза.

г) Начинаем с умножения \(0,4\) на \(5\), что даёт \(2\). Умножение десятичных дробей на целое число показывает, сколько будет в сумме. Далее умножаем \(2\) на \(0,01\), получая \(0,02\). Это уменьшение числа в \(100\) раз, так как \(0,01\) — сотая часть. Затем складываем \(0,02\) и \(0,28\), получая \(0,3\). Сложение десятичных дробей требует выравнивания количества знаков после запятой. В конце делим \(0,3\) на \(0,15\), что даёт \(2\). Деление десятичных дробей показывает, сколько раз число \(0,15\) помещается в \(0,3\).