ГДЗ по Математике 5 Класс Часть 2 Номер 820 Мнемозина Виленкин, Жохов — Подробные Ответы

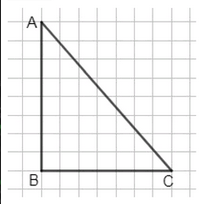
Начертите какой-нибудь треугольник и измерьте каждый его угол. Проверьте, что сумма градусных мер углов треугольника равна \(180^\circ\). Запомните это свойство углов треугольника.

Углы треугольника:
\( \angle A = 45^\circ \), \( \angle B = 90^\circ \), \( \angle C = 45^\circ \).

Сумма углов:
\( \angle A + \angle B + \angle C = 45 + 90 + 45 = 180^\circ \).

Ответ: верно.

Углы треугольника \( \triangle ABC \) даны как \( \angle A = 45^\circ \), \( \angle B = 90^\circ \), \( \angle C = 45^\circ \). Это значит, что угол \( B \) является прямым, так как его величина равна \( 90^\circ \). Такие углы характерны для прямоугольного треугольника, где один угол всегда равен \( 90^\circ \), а два других — острые. В данном случае углы \( A \) и \( C \) равны между собой и составляют по \( 45^\circ \), что указывает на равнобедренный прямоугольный треугольник, где два катета равны.

Для проверки правильности этой информации нужно найти сумму всех углов треугольника. По свойству геометрии сумма внутренних углов любого треугольника равна \( 180^\circ \). Поэтому складываем известные углы: \( \angle A + \angle B + \angle C = 45^\circ + 90^\circ + 45^\circ \). Сначала складываем углы \( 45^\circ \) и \( 90^\circ \), получая \( 135^\circ \), затем к этому результату прибавляем последний угол \( 45^\circ \), итого получаем \( 180^\circ \).

Таким образом, сумма углов равна \( 180^\circ \), что подтверждает правильность данных углов и соответствует основному свойству треугольника. Это доказывает, что треугольник \( ABC \) действительно прямоугольный с углами \( 45^\circ \), \( 90^\circ \) и \( 45^\circ \), и сумма его углов равна \( 180^\circ \), как и должно быть по определению. Ответ: верно.