ГДЗ по Математике 5 Класс Часть 2 Номер 815 Мнемозина Виленкин, Жохов — Подробные Ответы

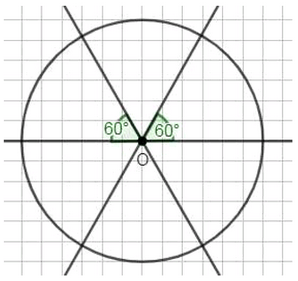
Начертите круг радиусом 3 см. Обозначьте его центр буквой \(O\). Проведите через точку \(O\) прямую \(AB\). С помощью транспортира разделите развёрнутые углы \(AOB\) с обеих сторон прямой на 3 равных угла. На сколько равных частей разделился круг?

Круг разделён на 6 равных частей.

Каждый центральный угол равен \( 60^\circ \).

Потому что полный круг \( 360^\circ \), а \( \frac{360^\circ}{6} = 60^\circ \).

Круг разделён на 6 равных частей, значит весь круг, который имеет угол в \(360^\circ\), разбит на 6 секторов с одинаковыми центральными углами. Чтобы найти угол каждого сектора, нужно разделить полный угол круга на количество частей. Таким образом, вычисляем угол одного сектора по формуле \( \frac{360^\circ}{6} \). Деление 360 на 6 даёт результат \(60^\circ\), значит каждый сектор имеет центральный угол \(60^\circ\).

Центральный угол — это угол, образованный двумя радиусами, исходящими из центра круга и ограничивающими сектор. Если круг разделён на равные части, то все эти углы равны между собой. На изображении видно, что угол между соседними радиусами равен \(60^\circ\), что подтверждает вычисление. Такое деление круга удобно использовать для построения правильных многоугольников, например, правильного шестиугольника, у которого все центральные углы равны \(60^\circ\).

Каждая из 6 частей круга называется сектором. Площадь каждого сектора пропорциональна его центральному углу. Если известна площадь всего круга, площадь одного сектора можно найти, умножив площадь круга на отношение угла сектора к полному углу круга, то есть на \(\frac{60^\circ}{360^\circ} = \frac{1}{6}\). Таким образом, круг, разделённый на 6 равных секторов, даёт 6 равных частей по площади и углу.