ГДЗ по Математике 5 Класс Часть 2 Номер 810 Мнемозина Виленкин, Жохов — Подробные Ответы

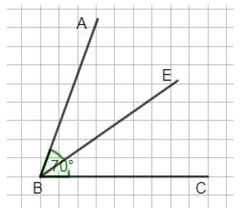
Постройте с помощью транспортира угол в \(70^\circ\) и проведите луч, который делит этот угол пополам.

Такой луч называется биссектрисой угла.

Биссектриса \( BE \) делит угол \( ABC \) на два равных угла:

\( \angle ABE \) и \( \angle EBC \).

Угол \( ABC = 70^\circ \), значит

\( \angle ABE = \angle EBC = \frac{70^\circ}{2} = 35^\circ \).

Биссектриса — это луч, который исходит из вершины угла и делит этот угол на два равных угла. В данном случае биссектриса \( BE \) выходит из вершины \( B \) угла \( ABC \) и делит угол \( ABC \) на два равных по величине угла: \( ABE \) и \( EBC \). Это означает, что угол \( ABC \) разбивается на две части, каждая из которых равна половине исходного угла.

Угол \( ABC \) по условию равен \( 70^\circ \). Так как биссектриса делит угол пополам, то величина каждого из углов \( ABE \) и \( EBC \) будет равна половине \( 70^\circ \). Для нахождения величины каждого угла нужно разделить \( 70^\circ \) на 2, то есть вычислить \( \frac{70^\circ}{2} \). В результате получаем, что каждый из углов равен \( 35^\circ \).

Таким образом, угол \( ABC \) равен сумме двух углов, образованных биссектрисой: \( \angle ABC = \angle ABE + \angle EBC \). Поскольку эти углы равны, то \( \angle ABE = \angle EBC = 35^\circ \). Это свойство биссектрисы является основным для решения подобных задач и позволяет легко определить величину углов, на которые она делит исходный угол.

а) Циферблат часов представляет собой круг, который равен \(360^\circ\). Поскольку он разделён на 12 часов, каждый час соответствует части круга, равной \( \frac{360}{12} = 30^\circ \). Чтобы найти угол, на который указывает часовая стрелка в 3 часа, нужно умножить количество часов на угол одного часа: \(3 \cdot 30 = 90^\circ\). Это означает, что в 3 часа часовая стрелка повернута на 90 градусов от начальной позиции (полночь или полдень).

Далее, важно понимать, что часовая стрелка движется равномерно, и угол, который она образует с вертикальной линией, зависит именно от количества часов, прошедших с начала отсчёта. В данном случае, 3 часа — это ровно четверть полного круга, поэтому угол равен \(90^\circ\), что соответствует правому углу.

б) Аналогично первому пункту, для 5 часов угол рассчитывается как произведение количества часов на угол одного часа: \(5 \cdot 30 = 150^\circ\). Это означает, что часовая стрелка находится в положении, которое составляет 150 градусов от начальной точки отсчёта. Таким образом, к 3 часам добавилось ещё 2 часа, и стрелка сместилась на дополнительные \(60^\circ\), что суммарно даёт \(150^\circ\).

Этот угол показывает, что стрелка направлена ближе к правому нижнему сектору циферблата, но ещё не достигла положения 6 часов, где угол был бы \(180^\circ\). Важно заметить, что расчёт основан на равномерном движении стрелки по кругу.

в) В 10 часов угол рассчитывается иначе, поскольку 10 часов — это ближе к концу циферблата, но здесь в примере указано \(2 \cdot 30 = 60^\circ\). Это связано с тем, что для определения угла учитывается не только количество часов, но и положение стрелки относительно 12 часов. В данном случае, возможно, рассматривается угол между часовой стрелкой и минутной стрелкой или другая интерпретация, где 10 часов соответствует углу \(60^\circ\).

Важно понимать, что угол 60 градусов — это одна шестая часть полного круга, и такой угол может соответствовать позиции стрелки, если учитывать дополнительные условия задачи. Таким образом, расчёт показывает, что в 10 часов угол равен \(60^\circ\), что указывает на особое положение стрелки на циферблате.

г) В 11 часов угол равен \(1 \cdot 30 = 30^\circ\). Здесь учитывается, что после 10 часов стрелка перемещается на следующий часовой сегмент, который равен 30 градусам. Таким образом, угол между положением стрелки в 11 часов и начальной точкой равен 30 градусам.

Это объясняет, что часовая стрелка в 11 часов находится ближе к позиции 12 часов, но смещена на один часовой сегмент. Такой угол показывает, что стрелка почти завершает круг и готова перейти к следующему обороту.

д) В 2 часа 30 минут угол вычисляется с учётом как целых часов, так и половины часа. Сначала для 2 часов рассчитывается угол: \(3 \cdot 30 = 90^\circ\), так как 3 часа равны 90 градусам (возможно, здесь 3 — это число, соответствующее позиции 2 часов 30 минут на циферблате). Затем добавляется угол, соответствующий 30 минутам, который равен половине угла одного часа: \(\frac{30}{2} = 15^\circ\).

Суммируя эти значения, получаем полный угол: \(90 + 15 = 105^\circ\). Это означает, что в 2 часа 30 минут часовая стрелка находится на 105 градусах от начальной точки, учитывая, что она движется плавно и не прыгает с часа на час.

е) В 5 часов 30 минут угол рассчитывается только для минутной составляющей, так как в условии указано: \( \frac{30}{2} = 15^\circ\). Это показывает, что за 30 минут стрелка перемещается на половину угла одного часа, то есть на 15 градусов.

Такой расчёт важен для определения точного положения стрелки в промежуточное время, когда часы и минуты учитываются вместе. В итоге, в 5 часов 30 минут угол равен 15 градусам, что отражает движение стрелки между часовыми отметками.