ГДЗ по Математике 5 Класс Часть 2 Номер 803 Мнемозина Виленкин, Жохов — Подробные Ответы

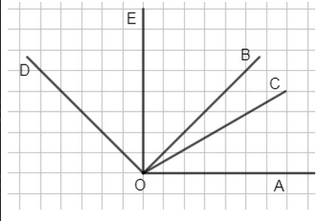
Начертите луч \(OA\). С помощью транспортира по одну сторону от луча \(OA\) постройте: \(\angle AOB = 45^\circ\), \(\angle AOC = 30^\circ\), \(\angle AOD = 135^\circ\), \(\angle AOE = 90^\circ\).

Угол между лучами:

Угол \( \angle AOB = 45^\circ \) (между горизонталью OA и лучом OB).

Угол \( \angle BOC = 15^\circ \) (между OB и OC).

Угол \( \angle COE = 60^\circ \) (между OC и OE).

Угол \( \angle DOE = 135^\circ \) (между OD и OE).

Сумма углов вокруг точки \( O \) равна \( 360^\circ \).

Угол \( \angle AOB = 45^\circ \) определяется как угол между лучом \(OA\), который лежит на горизонтальной оси, и лучом \(OB\), направленным вверх под углом к оси \(OX\). Чтобы найти этот угол, мы считаем количество клеток на сетке, которые луч \(OB\) поднимается вверх и смещается вправо. Поскольку луч \(OB\) поднимается на 3 клетки вверх и смещается на 3 клетки вправо, тангенс угла равен отношению этих величин, то есть \( \tan \alpha = \frac{3}{3} = 1 \). Из этого следует, что угол \( \alpha = 45^\circ \).

Угол \( \angle BOC = 15^\circ \) находится между лучами \(OB\) и \(OC\). Луч \(OC\) поднимается на 2 клетки вверх при смещении на 3 клетки вправо, поэтому тангенс угла \( \beta = \frac{2}{3} \). Для определения угла между двумя лучами нужно вычесть угол \( \beta \) из угла \( \alpha \), то есть \( 45^\circ — \arctan \frac{2}{3} \approx 15^\circ \). Таким образом, угол между лучами \(OB\) и \(OC\) равен примерно \(15^\circ\).

Угол \( \angle COE = 60^\circ \) измеряется между лучами \(OC\) и \(OE\), где \(OE\) вертикальный. Луч \(OC\) поднимается на 2 клетки вверх при смещении вправо на 3 клетки, а \(OE\) направлен строго вверх, то есть под углом \(90^\circ\) к горизонтали. Разница между углами равна \(90^\circ — \arctan \frac{2}{3} \approx 60^\circ\). Это показывает, что угол между \(OC\) и \(OE\) равен \(60^\circ\).

Угол \( \angle DOE = 135^\circ \) между лучами \(OD\) и \(OE\) можно найти, учитывая, что луч \(OD\) направлен влево и вверх под углом \(45^\circ\) к горизонтали в обратную сторону. Луч \(OE\) вертикален. Угол между ними равен сумме углов от горизонтали до \(OE\) и от горизонтали до \(OD\) в обратную сторону, то есть \(90^\circ + 45^\circ = 135^\circ\).

Сумма всех углов, исходящих из точки \(O\), равна \(360^\circ\), что подтверждает правильность вычисленных углов. В итоге углы \( \angle AOB = 45^\circ \), \( \angle BOC = 15^\circ \), \( \angle COE = 60^\circ \), \( \angle DOE = 135^\circ \) соответствуют положению лучей на координатной плоскости.