ГДЗ по Математике 5 Класс Часть 2 Номер 802 Мнемозина Виленкин, Жохов — Подробные Ответы

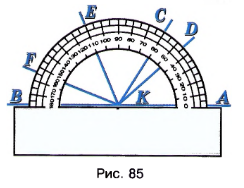
По рисунку 85 определите градусные меры углов:

а) \(AKD\), \(AKE\), \(AKF\);
б) \(BKF\), \(BKE\), \(BKC\), \(BKD\);
в) \(DKC\), \(DKE\), \(DKF\), \(CKE\), \(CKF\) и \(EKF\).

а) \( \angle AKD = 45^\circ; \quad \angle AKE = 110^\circ; \quad \angle AKF = 155^\circ. \)

б) \( \angle BKF = 25^\circ; \quad \angle BKE = 70^\circ; \quad \angle BKC = 120^\circ; \quad \angle BKD = 135^\circ. \)

в) \( \angle DKC = 60 — 45 = 15^\circ; \quad \angle DKE = 110 — 45 =\) \(= 65^\circ; \quad \angle DKF = 155 — 45 = 110^\circ; \)

\( \angle CKE = 110 — 60 = 50^\circ; \quad \angle CKF = 155 — 60 =\) \(= 95^\circ; \quad \angle EKF = 155 — 110 = 45^\circ. \)

а) В этом пункте даны углы \( \angle AKD = 45^\circ \), \( \angle AKE = 110^\circ \) и \( \angle AKF = 155^\circ \). Здесь важно понять, что углы связаны с точкой \(K\) и вершинами \(A\), \(D\), \(E\), \(F\). Значения углов даны напрямую, поэтому задача сводится к их запоминанию и пониманию, что они отражают определённые повороты или наклоны, исходящие из точки \(K\). Угол \( \angle AKD = 45^\circ \) показывает минимальный поворот между точками \(A\) и \(D\) относительно \(K\), тогда как \( \angle AKE = 110^\circ \) и \( \angle AKF = 155^\circ \) отражают более широкие углы, показывающие расположение точек \(E\) и \(F\) относительно \(A\) и \(K\).

Значения углов могут использоваться для дальнейших вычислений или построений, например, для нахождения других углов или проверки правильности построения фигуры. Важно отметить, что все углы измерены в градусах и лежат в диапазоне от \(0^\circ\) до \(180^\circ\), что характерно для углов между двумя лучами, исходящими из одной точки.

б) Во втором пункте представлены углы \( \angle BKF = 25^\circ \), \( \angle BKE = 70^\circ \), \( \angle BKC = 120^\circ \), \( \angle BKD = 135^\circ \). Эти углы также связаны с точкой \(K\), но теперь вершиной является точка \(B\). Значения углов показывают, как точки \(F\), \(E\), \(C\), \(D\) расположены относительно \(B\) и \(K\). Например, угол \( \angle BKF = 25^\circ \) — самый маленький, что говорит о близком расположении точек \(B\) и \(F\) относительно \(K\).

Значения углов в этом пункте увеличиваются от \(25^\circ\) до \(135^\circ\), что позволяет представить последовательное расположение точек вокруг \(K\). Такая информация может быть полезна для анализа взаимного расположения точек или для вычисления дополнительных углов, если известно, что сумма углов вокруг точки равна \(360^\circ\).

в) В третьем пункте выполняются вычисления углов на основе разности данных значений. Например, \( \angle DKC = 60^\circ — 45^\circ = 15^\circ \). Здесь берутся два угла и вычитается меньший из большего, чтобы найти угол между двумя лучами, исходящими из точки \(K\). Аналогично для остальных углов: \( \angle DKE = 110^\circ — 45^\circ = 65^\circ \), \( \angle DKF = 155^\circ — 45^\circ = 110^\circ \).

Далее вычисляются углы \( \angle CKE = 110^\circ — 60^\circ = 50^\circ \), \( \angle CKF = 155^\circ — 60^\circ = 95^\circ \), и \( \angle EKF = 155^\circ — 110^\circ = 45^\circ \). Эти вычисления основаны на разности углов, что позволяет определить величину угла между двумя направлениями, заданными исходными значениями. Такой подход часто используется в геометрии для нахождения углов между лучами или сторонами, если известны ориентировочные углы относительно одной точки.