ГДЗ по Математике 5 Класс Часть 2 Номер 792 Мнемозина Виленкин, Жохов — Подробные Ответы

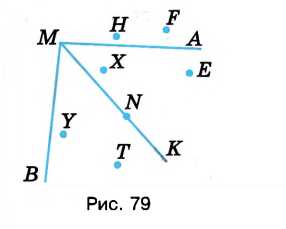
Какие из отмеченных на рисунке 79 точек лежат внутри угла \(AMK\)? Какая точка лежит внутри угла \(AMB\), но вне угла \(AMK\)? Какие точки лежат на сторонах угла \(AMK\)?

а) Внутри угла \( AMK \) лежат точки \( X \) и \( E \).

б) Внутри угла \( AMB \), но вне угла \( AMK \), лежит точка \( Y \).

в) На сторонах угла \( AMK \) лежит точка \( N \).

а) Внутри угла \( AMK \) лежат точки \( X \) и \( E \). Это означает, что если рассмотреть лучи, образующие угол \( AMK \), то точки \( X \) и \( E \) расположены в области между этими лучами, не выходя за их пределы. Такое расположение указывает на то, что обе точки находятся в пространстве, ограниченном углом, то есть внутри него. Для проверки этого можно мысленно провести лучи \( MA \) и \( MK \) и убедиться, что точки \( X \) и \( E \) расположены так, что отрезки, соединяющие их с вершиной \( M \), не пересекают внешнюю область угла.

Это важно, так как понятие «внутри угла» подразумевает, что точка лежит в том секторе плоскости, который ограничен двумя лучами, исходящими из одной точки. Если точка лежит вне этого сектора, ее нельзя считать внутренней для данного угла. Таким образом, точки \( X \) и \( E \) удовлетворяют условию внутреннего расположения относительно угла \( AMK \).

б) Точка \( Y \) лежит внутри угла \( AMB \), но вне угла \( AMK \). Это значит, что точка находится в пространстве, ограниченном лучами, образующими угол \( AMB \), однако при этом она не попадает в пространство угла \( AMK \). Угол \( AMB \) шире или отличается от угла \( AMK \), поэтому точка \( Y \) расположена в той части плоскости, которая входит в угол \( AMB \), но не пересекается с областью угла \( AMK \).

Для понимания этого можно представить себе, что угол \( AMB \) включает в себя угол \( AMK \) и некоторую дополнительную область. Точка \( Y \) находится именно в этой дополнительной области, что подтверждается условием, что она лежит внутри \( AMB \), но вне \( AMK \). Это важно для различения областей, ограниченных разными углами с общей вершиной \( M \).

в) Точка \( N \) лежит на стороне угла \( AMK \). Это означает, что \( N \) расположена на одном из лучей, образующих угол \( AMK \), то есть либо на луче \( MA \), либо на луче \( MK \). Положение точки \( N \) на стороне угла указывает на то, что она принадлежит границе угла, а не его внутренней области или внешней.

Такое расположение точки важно для понимания геометрических свойств угла, так как точки на сторонах угла могут использоваться для построений и доказательств, связанных с углами и их мерами. В данном случае точка \( N \) служит примером точки, находящейся именно на границе угла \( AMK \), что отличает ее от точек, лежащих внутри угла или вне его.