ГДЗ по Математике 5 Класс Часть 2 Номер 783 Мнемозина Виленкин, Жохов — Подробные Ответы

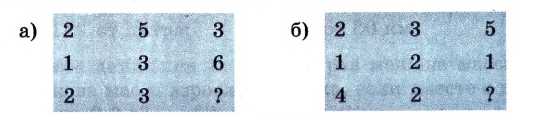
Найдите пропущенное число:

а) Найдем сумму чисел в первых двух строках:
\(2 + 5 + 3 = 10\); \(1 + 3 + 6 = 10\).
Значит, в третьей строке сумма трёх чисел должна быть равна 10:
\(10 — 2 — 3 = 5\).
То есть, пропущенное число равно 5.
Ответ: 5.

б) Найдем сумму чисел в первых двух столбцах:
\(2 + 1 + 4 = 7\); \(3 + 2 + 2 = 7\).
Значит, в третьем столбце сумма трёх чисел должна быть равна 7:
\(7 — 5 — 1 = 1\).
То есть, пропущенное число равно 1.
Ответ: 1.

а) Для начала определим сумму чисел в первых двух строках. В первой строке даны числа 2, 5 и 3, и их сумма равна \(2 + 5 + 3 = 10\). Во второй строке числа 1, 3 и 6, и их сумма также равна \(1 + 3 + 6 = 10\). Поскольку сумма чисел в обеих строках равна 10, можно предположить, что сумма чисел в третьей строке тоже должна быть равна 10, чтобы сохранить закономерность.

В третьей строке известны два числа — 2 и 3, а третье число пропущено. Чтобы найти это число, нужно из общей суммы 10 вычесть сумму известных чисел: \(10 — 2 — 3 = 5\). Это значит, что пропущенное число равно 5. Таким образом, сумма всех трёх чисел в третьей строке становится равной 10, что соответствует условию задачи.

Такой подход позволяет восстановить пропущенное число, исходя из равенства сумм по строкам. Это важно, поскольку в задаче предполагается, что сумма чисел в каждой строке одинаковая, и мы используем это свойство для нахождения неизвестного элемента.

б) Рассмотрим теперь столбцы. Сначала найдем сумму чисел в первых двух столбцах. В первом столбце числа 2, 1 и 4, их сумма равна \(2 + 1 + 4 = 7\). Во втором столбце числа 3, 2 и 2, и их сумма также равна \(3 + 2 + 2 = 7\). Таким образом, сумма чисел в первых двух столбцах равна 7, и можно предположить, что сумма чисел в третьем столбце тоже должна быть равна 7.

В третьем столбце известны два числа — 5 и 1, а третье число отсутствует. Чтобы найти это число, из общей суммы 7 вычитаем сумму известных чисел: \(7 — 5 — 1 = 1\). Следовательно, пропущенное число равно 1. Это позволяет сохранить равенство сумм по столбцам и завершить заполнение таблицы.

Использование равенства сумм по строкам и столбцам — ключевой метод решения этой задачи. Он позволяет определить недостающие элементы, исходя из заданных условий, и обеспечивает целостность и правильность заполнения числовой таблицы.