ГДЗ по Математике 5 Класс Часть 2 Номер 776 Мнемозина Виленкин, Жохов — Подробные Ответы

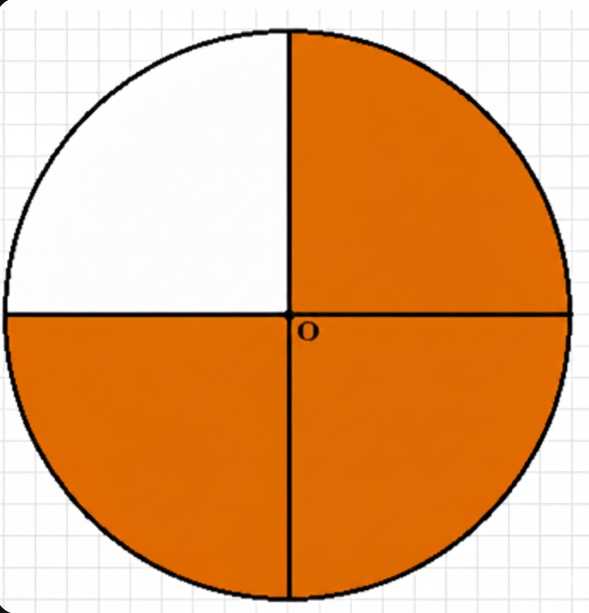
Начертите круг с центром О и радиусом 4,5 см. Разделите круг на четыре доли и закрасьте \(\frac{3}{4}\) круга.

Рассмотрим круг с центром О и радиусом 4,5 см. Разделим круг на четыре равные части (четверти).

Закрасим 3 из 4 частей, что соответствует \( \frac{3}{4} \) круга.

Таким образом, закрашено 3 четверти круга, а одна четверть остается незакрашенной, как показано на рисунке.

Рассмотрим круг с центром в точке О и радиусом 4,5 см. Радиус — это отрезок, соединяющий центр круга с любой точкой на его окружности, в данном случае длина радиуса равна 4,5 см. Чтобы выполнить задание, необходимо сначала начертить круг с заданным радиусом, используя циркуль или другой инструмент, позволяющий провести ровный круг с точным радиусом.

Далее круг нужно разделить на четыре равные части. Для этого через центр О проводят две взаимно перпендикулярные прямые, которые пересекаются в точке О и делят круг на четыре четверти. Каждая такая четверть является сектором круга с центральным углом 90 градусов, так как полный круг равен 360 градусам, а \( \frac{360}{4} = 90 \). Таким образом, мы получаем четыре равных сектора, каждый из которых занимает одну четверть всего круга.

Задача требует закрасить 3 из 4 частей, то есть \( \frac{3}{4} \) круга. Это значит, что три сектора из четырех должны быть окрашены, а один оставить незакрашенным. В итоге, площадь закрашенной части равна \( \frac{3}{4} \) площади всего круга. Если обозначить площадь круга через \( S \), то площадь закрашенной части будет равна \( \frac{3}{4} S \). Такая визуализация помогает понять, какую часть круга занимает закрашенная область, и наглядно демонстрирует дробь \( \frac{3}{4} \) в геометрическом виде.