ГДЗ по Математике 5 Класс Часть 2 Номер 774 Мнемозина Виленкин, Жохов — Подробные Ответы

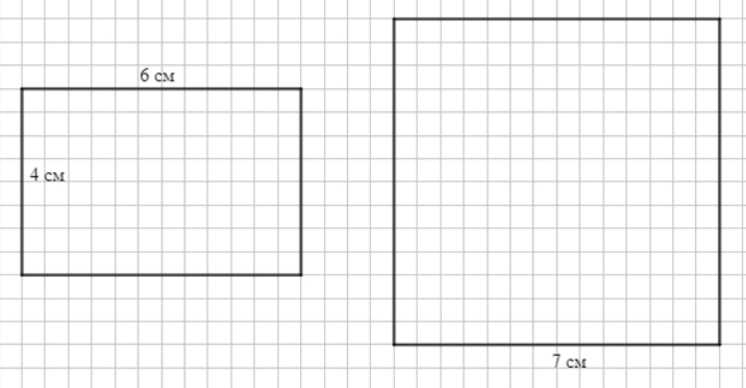
Начертите прямоугольник со сторонами 6 см и 4 см и квадрат со стороной 7 см.

1) Начертим прямоугольник со сторонами 6 см и 4 см. Его стороны будут равны \(6 \text{ см}\) и \(4 \text{ см}\).

2) Начертим квадрат со стороной 7 см. Все стороны квадрата равны \(7 \text{ см}\).

1) Начертим прямоугольник со сторонами 6 см и 4 см. Прямоугольник — это четырёхугольник, у которого противоположные стороны равны и все углы прямые, то есть равны \(90^\circ\). В данном случае одна пара противоположных сторон будет иметь длину \(6 \text{ см}\), а другая — \(4 \text{ см}\). Для построения начертим сначала одну сторону длиной \(6 \text{ см}\), затем под прямым углом к ней проведём сторону длиной \(4 \text{ см}\). После этого замкнём фигуру, проведя ещё две стороны, равные соответственно \(6 \text{ см}\) и \(4 \text{ см}\).

Прямоугольник обладает важным свойством — его площадь вычисляется по формуле произведения длины на ширину, то есть \(S = 6 \times 4 = 24 \text{ см}^2\). Это означает, что площадь фигуры равна произведению длин двух соседних сторон. Также периметр прямоугольника равен сумме всех сторон, то есть \(P = 2 \times (6 + 4) = 20 \text{ см}\). Эти характеристики помогают понять, как именно расположены стороны и какую площадь занимает фигура на плоскости.

2) Начертим квадрат со стороной 7 см. Квадрат — это частный случай прямоугольника, у которого все четыре стороны равны, а все углы равны \(90^\circ\). В нашем случае каждая сторона равна \(7 \text{ см}\), поэтому при построении достаточно начертить одну сторону длиной \(7 \text{ см}\), а затем провести три другие стороны той же длины под прямыми углами друг к другу, чтобы замкнуть фигуру. Квадрат является правильным четырёхугольником, что означает равенство всех сторон и углов.

Площадь квадрата вычисляется по формуле \(S = 7^2 = 49 \text{ см}^2\), то есть квадрат длины его стороны. Периметр квадрата равен сумме длин всех четырёх сторон, то есть \(P = 4 \times 7 = 28 \text{ см}\). Эти формулы позволяют определить, сколько места занимает квадрат на плоскости и какова длина его границ. Важно понимать, что квадрат — это равносторонний и равнопрямоугольный многоугольник, что отличает его от прямоугольника с разными сторонами.