ГДЗ по Математике 5 Класс Часть 2 Номер 772 Мнемозина Виленкин, Жохов — Подробные Ответы

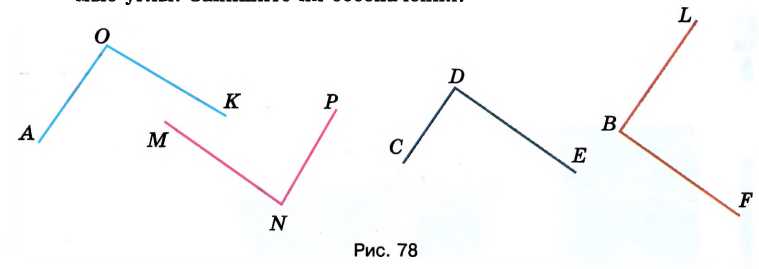
С помощью чертёжного треугольника найдите на рисунке 78 прямые углы. Запишите их обозначения.

\( \angle CDE = 90^\circ \) и \( \angle LBF = 90^\circ \).

На данном чертеже с помощью чертёжного треугольника определяются прямые углы, то есть углы, равные \(90^\circ\). Прямой угол характеризуется тем, что его стороны перпендикулярны друг другу. Это значит, что линии, образующие такой угол, пересекаются под углом ровно \(90^\circ\), что является основным признаком прямого угла. В нашем случае это позволяет определить углы \( \angle CDE \) и \( \angle LBF \) как прямые, так как по условию они равны \(90^\circ\).

Угол \( \angle CDE \) обозначает угол, вершина которого находится в точке \(D\), а стороны проходят через точки \(C\) и \(E\). Поскольку \( \angle CDE = 90^\circ \), это означает, что линии \(DC\) и \(DE\) взаимно перпендикулярны. Аналогично, угол \( \angle LBF \) с вершиной в точке \(B\) образован сторонами, проходящими через точки \(L\) и \(F\), и он также равен \(90^\circ\). Это подтверждает, что линии \(BL\) и \(BF\) тоже перпендикулярны.

Использование чертёжного треугольника позволяет точно измерить и проверить эти углы, так как он специально предназначен для построения и проверки углов в \(90^\circ\). Таким образом, на рисунке выделены именно два прямых угла — \( \angle CDE \) и \( \angle LBF \), что соответствует условию задачи и подтверждается измерениями с помощью инструмента. Эти углы важны для понимания геометрических соотношений на чертеже и дальнейших построений.