ГДЗ по Математике 5 Класс Часть 2 Номер 771 Мнемозина Виленкин, Жохов — Подробные Ответы

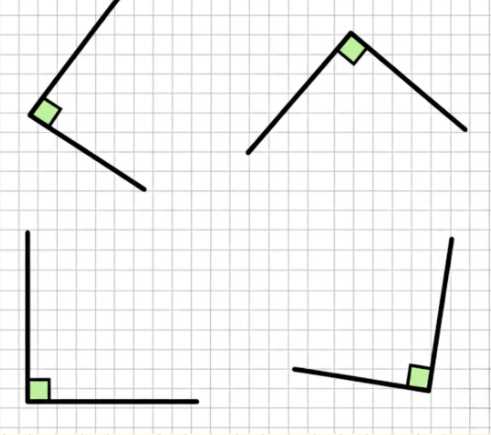
Изобразите с помощью чертёжного треугольника 4 прямых угла в разных положениях.

Чертёжный треугольник имеет прямой угол 90°. Чтобы получить 4 прямых угла в разных положениях, нужно расположить треугольник так, чтобы его прямой угол был направлен вверх, вниз, влево и вправо.

1) Прямой угол направлен вверх.
2) Прямой угол направлен вправо.
3) Прямой угол направлен вниз.
4) Прямой угол направлен влево.

Таким образом, поворачивая треугольник на 90°, 180°, 270° и 0° (исходное положение), получаем 4 прямых угла в разных положениях.

Чертёжный треугольник — это инструмент, который обычно имеет один прямой угол равный \(90^\circ\) и два острых угла. Для выполнения задания необходимо показать четыре различных положения этого прямого угла. Прямой угол — это угол, равный \(90^\circ\), и он всегда образуется между двумя сторонами треугольника. Повернув треугольник, можно изменить ориентацию этого угла, сохраняя его величину.

Первое положение — исходное, когда прямой угол направлен вверх. В этом случае одна сторона треугольника расположена вертикально, а другая — горизонтально, образуя угол \(90^\circ\) в верхней части фигуры. Это положение часто используется для построения вертикальных и горизонтальных линий, что удобно при черчении. Второе положение достигается поворотом треугольника на \(90^\circ\) по часовой стрелке, тогда прямой угол будет направлен вправо. Здесь одна сторона станет горизонтальной, а другая — вертикальной, но уже с другой стороны, сохраняя угол \(90^\circ\).

Для третьего положения треугольник поворачивается ещё на \(90^\circ\), то есть на \(180^\circ\) от исходного положения. Теперь прямой угол направлен вниз, и стороны треугольника располагаются так, что угол \(90^\circ\) смотрит вниз. Это позволяет создавать прямые углы в нижней части чертежа. Четвёртое положение — поворот на \(270^\circ\) или на \(90^\circ\) против часовой стрелки от исходного, когда прямой угол направлен влево. Таким образом, меняется ориентация прямого угла, но его величина остаётся неизменной. Повороты треугольника на \(90^\circ\) обеспечивают четыре уникальных положения прямого угла, что и требуется в задании.

Таким образом, для получения четырёх прямых углов в разных положениях нужно просто повернуть чертёжный треугольник последовательно на углы \(0^\circ\), \(90^\circ\), \(180^\circ\) и \(270^\circ\). При каждом повороте прямой угол сохраняет свою величину \(90^\circ\), но меняет направление, позволяя изобразить прямой угол в четырёх различных ориентациях. Это простой и эффективный способ показать разнообразие положений прямого угла с помощью одного инструмента.