ГДЗ по Математике 5 Класс Часть 2 Номер 770 Мнемозина Виленкин, Жохов — Подробные Ответы

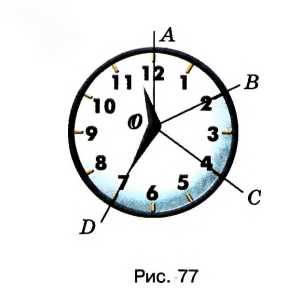
Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а ещё за 15 мин — на угол COD. Сравните углы \(AOB\) и \(BOC\), \(BOC\) и \(COD\), \(AOC\) и \(AOB\), \(AOC\) и \(COD\) (рис. 77).

Угол, на который повернулась минутная стрелка за 10 мин:
\( \angle AOB = 10 \times 6^\circ = 60^\circ \).

За следующие 10 мин угол:
\( \angle BOC = 10 \times 6^\circ = 60^\circ \).

За ещё 15 мин угол:
\( \angle COD = 15 \times 6^\circ = 90^\circ \).

Сравним углы:

\( \angle AOB = \angle BOC \) (оба равны 60°);

\( \angle BOC < \angle COD \) (60° < 90°); \( \angle AOC = \angle AOB + \angle BOC = 60^\circ + 60^\circ = 120^\circ \); \( \angle AOC > \angle AOB \) (120° > 60°);

\( \angle AOC > \angle COD \) (120° > 90°).

Минутная стрелка часов за 10 минут поворачивается на угол, который можно найти, учитывая, что за 1 минуту стрелка проходит угол в 6 градусов, так как полный круг равен 360 градусам, а минутная стрелка делает полный оборот за 60 минут. Следовательно, угол поворота за 10 минут равен \( 10 \times 6^\circ = 60^\circ \). Этот угол обозначен как \( \angle AOB \).

За следующие 10 минут минутная стрелка также поворачивается на угол, равный \( 10 \times 6^\circ = 60^\circ \). Этот угол обозначен как \( \angle BOC \). Поскольку оба угла равны 60 градусам, можно сделать вывод, что \( \angle AOB = \angle BOC \).

За последующие 15 минут стрелка поворачивается на угол \( 15 \times 6^\circ = 90^\circ \), который обозначен как \( \angle COD \). Этот угол больше, чем углы, пройденные за предыдущие 10 минут, поэтому \( \angle BOC < \angle COD \). Угол \( \angle AOC \) — это сумма углов \( \angle AOB \) и \( \angle BOC \), так как точка \( O \) является вершиной, а точки \( A, B, C \) расположены по порядку движения стрелки. Следовательно, \( \angle AOC = \angle AOB + \angle BOC = 60^\circ + 60^\circ = 120^\circ \). Поскольку \( \angle AOC = 120^\circ \), а \( \angle AOB = 60^\circ \), то \( \angle AOC > \angle AOB \). Аналогично, сравнивая \( \angle AOC \) и \( \angle COD \), получаем, что \( 120^\circ > 90^\circ \), значит \( \angle AOC > \angle COD \). Таким образом, все сравнения углов подтверждаются вычислениями, основанными на углах, которые минутная стрелка проходит за заданные промежутки времени.