ГДЗ по Математике 5 Класс Часть 2 Номер 767 Мнемозина Виленкин, Жохов — Подробные Ответы

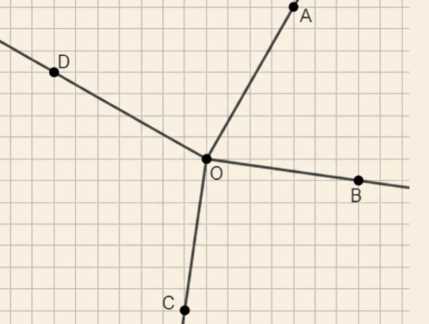
Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость?

Уголов: \( \angle AOB; \ \angle AOC; \ \angle AOD; \ \angle BOC; \ \angle BOD; \ \angle COD \).

Данные лучи делят плоскость на четыре части.

Углы \( \angle AOB \), \( \angle AOC \), \( \angle AOD \), \( \angle BOC \), \( \angle BOD \), \( \angle COD \) образованы лучами, исходящими из одной точки \( O \). Эти лучи делят плоскость на несколько частей, каждая из которых ограничена двумя соседними лучами. При этом каждый угол — это фигура, образованная двумя лучами с общим началом в точке \( O \).

Рассмотрим подробнее, как именно делятся углы. Лучи \( OA \), \( OB \), \( OC \), \( OD \) исходят из точки \( O \) и расположены так, что между ними образуются углы \( \angle AOB \), \( \angle BOC \), \( \angle COD \), \( \angle DOA \). Кроме того, можно рассматривать углы, образованные лучами, которые не соседствуют напрямую, например, \( \angle AOC \), \( \angle BOD \). Все эти углы вместе охватывают всю плоскость вокруг точки \( O \).

Данные лучи делят плоскость на четыре части, так как каждая пара соседних лучей образует угол, а сумма всех этих углов равна \( 360^\circ \). Таким образом, лучи \( OA \), \( OB \), \( OC \), \( OD \) разбивают плоскость на четыре угловые области, каждая из которых является частью плоскости, ограниченной двумя лучами. Это означает, что лучи не пересекаются друг с другом, кроме точки \( O \), и вместе они создают четыре сектора, в каждом из которых расположен один из углов \( \angle AOB \), \( \angle BOC \), \( \angle COD \), \( \angle DOA \).