ГДЗ по Математике 5 Класс Часть 2 Номер 728 Мнемозина Виленкин, Жохов — Подробные Ответы

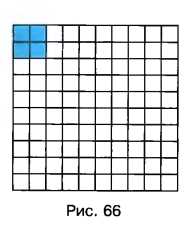
Двор разбит на 100 равных частей. Часть площади двора, закрашенная на рисунке 66, отведена под стоянку машин. Найдите площадь двора, если стоянка занимает 146,4 м\(^2\).

1) На рисунке показано, что стоянка занимает 4 доли из 100, то есть, 4 %.

2) Так как стоянка занимает 146,4 м\(^{2}\), а это 4 %, то 1 % равен: \(146{,}4 : 4 = 36{,}6\) (м\(^{2}\)).

3) Площадь двора равна: \(36{,}6 \cdot 100 = 3660\) (м\(^{2}\)).

Ответ: 3660 м\(^{2}\).

1) На рисунке показано, что стоянка занимает 4 доли из 100, то есть 4 %. Это означает, что площадь, занимаемая стоянкой, составляет 4 % от общей площади двора. Процентное выражение помогает нам понять, какую часть от целого занимает стоянка, где целое — это весь двор, а часть — это стоянка. Таким образом, если весь двор считать за 100 %, то стоянка — это именно 4 % от этого количества.

Процент — это способ выразить отношение части к целому в сотых долях. Здесь 4 доли из 100 — это и есть 4 %. Это важное понимание, потому что далее мы будем использовать это соотношение для вычисления площади всего двора, зная площадь стоянки.

2) Из условия известно, что площадь стоянки равна 146,4 м\(^{2}\), и это соответствует 4 % от площади всего двора. Чтобы найти, чему равен 1 % площади двора, нужно разделить площадь стоянки на 4, так как 146,4 м\(^{2}\) — это 4 %. Выполним деление: \(146{,}4 : 4 = 36{,}6\) м\(^{2}\). Это значит, что 1 % площади двора равен 36,6 м\(^{2}\).

Таким образом, мы нашли, сколько квадратных метров занимает 1 % всей площади двора. Это промежуточный и очень важный шаг, потому что теперь, зная площадь, соответствующую 1 %, мы можем вычислить площадь всего двора, умножив это значение на 100.

3) Чтобы найти площадь всего двора, нужно умножить площадь, соответствующую 1 %, на 100, так как весь двор — это 100 %. Следовательно, площадь двора равна \(36{,}6 \cdot 100 = 3660\) м\(^{2}\). Это и есть искомая площадь всего двора.

Таким образом, используя информацию о том, что стоянка занимает 4 % площади двора и зная её площадь в квадратных метрах, мы последовательно вычислили площадь, соответствующую 1 %, а затем нашли общую площадь двора. Ответ: 3660 м\(^{2}\).