ГДЗ по Математике 5 Класс Часть 2 Номер 725 Мнемозина Виленкин, Жохов — Подробные Ответы

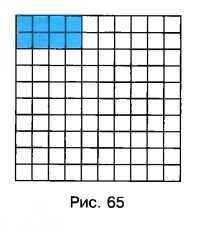
Поле на рисунке 65 разбито на 100 долей. Закрашенная на рисунке часть засеяна горохом. Найдите площадь всего поля, если горохом засеяно 24,8 га.

1) На рисунке показано, что горохом засеяно 8 долей из 100, то есть, 8 %.

2) Так как горохом засеяно 24,8 га, а это 8 %, то 1 % равен: \(24,8 \div 8 = 3,1\) (га).

3) Площадь всего поля равна: \(3,1 \times 100 = 310\) (га).

Ответ: 310 га.

1) На рисунке указано, что горохом засеяно 8 долей из 100. Это означает, что из всего поля, которое условно разделено на 100 равных частей, горох занимает 8 частей. Таким образом, доля, занятая горохом, выражается в процентах как 8 %. Процент — это способ показать отношение части к целому, выраженное в сотых долях, поэтому 8 частей из 100 — это и есть 8 %.

Во многих задачах проценты помогают быстро понять, какую часть от общего объема занимает какая-то величина. Здесь важно запомнить, что 8 % — это то же самое, что 8 из 100 или 0,08 в десятичной форме. Это ключевой момент, который позволит дальше вычислить площадь всего поля, зная площадь, занятая горохом.

2) Из условия известно, что площадь, засеянная горохом, равна 24,8 га, и эта площадь составляет 8 % от всего поля. Чтобы найти, сколько гектаров соответствует 1 %, нужно разделить площадь гороха на 8. Деление 24,8 на 8 даёт результат \(24,8 \div 8 = 3,1\) га. Это значит, что каждый 1 % площади поля равен 3,1 гектара.

Этот шаг важен для того, чтобы перейти от части к целому. Зная площадь, соответствующую 1 %, можно легко вычислить площадь всего поля, умножив найденное значение на 100. Такой подход часто применяется при решении задач с процентами, когда известна часть от целого, а нужно найти весь объем или площадь.

3) Теперь, когда мы знаем, что 1 % поля равен 3,1 га, можно найти площадь всего поля, умножив 3,1 на 100, так как 100 % — это весь участок. Получаем \(3,1 \times 100 = 310\) га. Это и есть искомая площадь всего поля.

Таким образом, используя информацию о том, что 8 % поля — это 24,8 га, мы последовательно нашли площадь, соответствующую 1 %, а затем вычислили площадь всего поля. Итоговый ответ — 310 га — показывает, насколько большой участок используется под посевы, если 8 % от него занимают 24,8 га гороха.