ГДЗ по Математике 5 Класс Часть 2 Номер 717 Мнемозина Виленкин, Жохов — Подробные Ответы

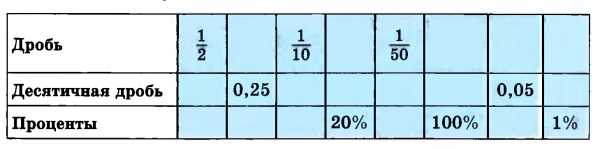
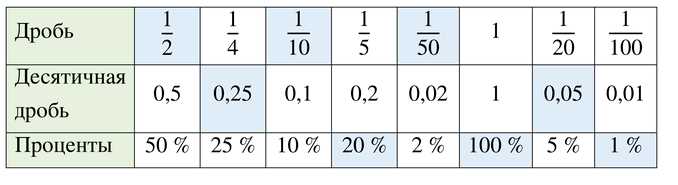
Заполните таблицу:

Для \( \frac{1}{10} \): десятичная дробь равна \(0,1\), проценты — \(10 \%\), так как \( \frac{1}{10} = 0,1 = 10\% \).

Для \( \frac{1}{50} \): десятичная дробь равна \(0,02\), проценты — \(2 \%\), так как \( \frac{1}{50} = 0,02 = 2\% \).

Для начала рассмотрим, как перевести дробь \(\frac{1}{10}\) в десятичную дробь. Дробь \(\frac{1}{10}\) означает, что единица делится на десять равных частей, и берется одна такая часть. Если мы выполним деление 1 на 10, то получим число \(0,1\). Это и есть десятичное представление дроби \(\frac{1}{10}\). Таким образом, десятичная дробь — это просто результат деления числителя на знаменатель, записанный в десятичной форме.

Теперь перейдем к переводу десятичной дроби \(0,1\) в проценты. Чтобы найти процентное значение числа, нужно умножить его на 100 и добавить знак процента. В нашем случае это будет \(0,1 \times 100 = 10\). Следовательно, дробь \(\frac{1}{10}\) равна 10 процентам, что можно записать как \(10 \%\). Этот способ перевода универсален для всех десятичных дробей: умножаем на 100 и добавляем знак процента.

Рассмотрим аналогично дробь \(\frac{1}{50}\). Деление 1 на 50 дает десятичную дробь \(0,02\), так как \(1 \div 50 = 0,02\). Это означает, что единица разделена на 50 равных частей, и одна часть составляет 0,02. Чтобы перевести это в проценты, умножаем \(0,02\) на 100, получая \(2\). Значит, \(\frac{1}{50}\) равно \(2 \%\). Таким образом, для любых дробей перевод в десятичные дроби и проценты выполняется через деление и умножение на 100 соответственно.