ГДЗ по Математике 5 Класс Часть 2 Номер 70 Мнемозина Виленкин, Жохов — Подробные Ответы

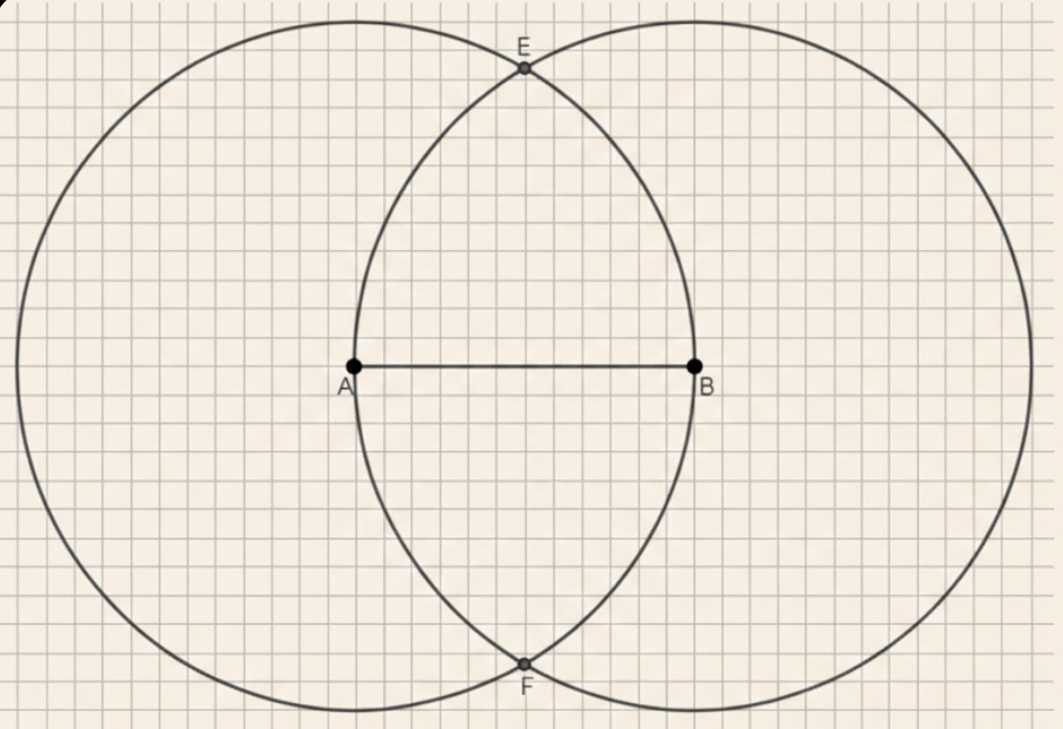
Начертите отрезок \(AB = 6\) см. Найдите точки, которые удалены от \(A\) и от \(B\) на 6 см.

Точки \(E\) и \(F\) — это точки пересечения окружностей с центрами в точках \(A\) и \(B\), радиус которых равен 6 см.

Отрезок \(AB\) — это основание равнобедренного треугольника \(AEF\) или \(BEF\), где \(AE = BE = 6\) см.

Длина \(AB = 6\) см (по рисунку и условию).

Высота \(EF\) в треугольнике \(AEF\) найдется из прямоугольного треугольника с гипотенузой 6 см и одним катетом 3 см (половина \(AB\)):

\(EF = \sqrt{6^2 — 3^2} = \sqrt{36 — 9} = \sqrt{27} = 3\sqrt{3}\) см.

Точки \(E\) и \(F\) являются точками пересечения двух окружностей с центрами в точках \(A\) и \(B\). Каждая из этих окружностей имеет радиус 6 см, что означает, что расстояние от центра окружности до любой точки на ней равно 6 см. В данном случае, поскольку \(E\) и \(F\) лежат на обеих окружностях, они находятся на одинаковом расстоянии 6 см от точек \(A\) и \(B\). Это ключевое наблюдение, которое позволяет рассматривать треугольники \(AEF\) и \(BEF\) как равнобедренные с равными сторонами, равными радиусу окружности.

Отрезок \(AB\) является основанием равнобедренного треугольника \(AEF\) (или \(BEF\)), где стороны \(AE\) и \(BE\) равны 6 см. По условию и изображению видно, что длина отрезка \(AB\) равна 6 см. Таким образом, \(AB\) — это основание треугольника с длиной 6 см, а \(AE\) и \(BE\) — равные боковые стороны, каждая длиной 6 см. В этом треугольнике можно провести высоту \(EF\), которая будет перпендикулярна к \(AB\) и делить его пополам, то есть точка пересечения высоты с \(AB\) делит отрезок \(AB\) на два равных отрезка по 3 см.

Для нахождения длины высоты \(EF\) рассмотрим прямоугольный треугольник, образованный высотой \(EF\), половиной основания \(AB\) (то есть отрезком длиной 3 см) и боковой стороной \(AE\) (гипотенузой) длиной 6 см. По теореме Пифагора длина высоты \(EF\) равна корню из разности квадрата гипотенузы и квадрата одного из катетов: \(EF = \sqrt{6^2 — 3^2} = \sqrt{36 — 9} = \sqrt{27} = 3\sqrt{3}\) см. Эта величина показывает расстояние между точками пересечения окружностей \(E\) и \(F\), которые находятся выше и ниже отрезка \(AB\).

Таким образом, мы использовали свойства равенства радиусов окружностей и равнобедренности треугольника, чтобы определить высоту \(EF\). Этот подход позволяет точно определить расстояние между точками пересечения окружностей, исходя из известных расстояний между центрами и радиусов. В итоге, длина отрезка \(EF\) равна \(3\sqrt{3}\) см.