ГДЗ по Математике 5 Класс Часть 2 Номер 7 Мнемозина Виленкин, Жохов — Подробные Ответы

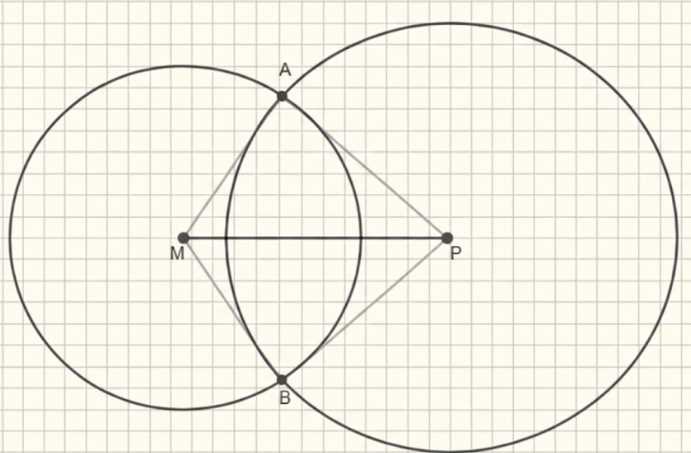
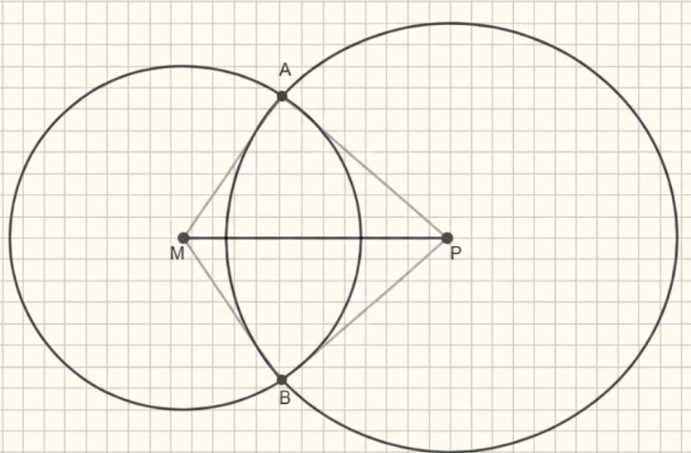
Начертите отрезок \(MP\), равный 6 см. Найдите две точки \(A\) и \(B\), которые находились бы на расстоянии 4 см от точки \(M\) и 5 см от точки \(P\).

Точки \(A\) и \(B\) лежат на пересечении двух окружностей с центрами в точках \(M\) и \(P\).

Расстояние между центрами \(MP = 9\) см (по сетке).

Радиус окружности с центром \(M\) равен 4 см, радиус окружности с центром \(P\) равен 5 см.

Точки \(A\) и \(B\) находятся на расстоянии 4 см от точки \(M\) и 5 см от точки \(P\), значит они лежат на пересечении этих двух окружностей.

Ответ: \(A\) и \(B\) — точки пересечения окружностей с радиусами 4 см и 5 см и центрами в точках \(M\) и \(P\) соответственно.

Точки \(A\) и \(B\) расположены на пересечении двух окружностей с центрами в точках \(M\) и \(P\). Каждая из этих точек лежит на расстоянии 4 см от точки \(M\) и 5 см от точки \(P\), то есть они принадлежат одновременно окружности с радиусом 4 см, построенной вокруг \(M\), и окружности с радиусом 5 см, построенной вокруг \(P\). Это означает, что точки \(A\) и \(B\) являются общими точками двух данных окружностей.

Расстояние между центрами окружностей \(M\) и \(P\) равно 9 см, что видно по сетке на рисунке. Для того чтобы окружности пересекались, сумма радиусов должна быть не меньше расстояния между центрами, а разность радиусов не должна превышать это расстояние. В нашем случае \(4 + 5 = 9\), что равно расстоянию между центрами, значит окружности касаются друг друга в двух точках — \(A\) и \(B\). Таким образом, эти точки лежат на линии пересечения двух кругов и удовлетворяют условию быть на заданных расстояниях от \(M\) и \(P\).

Положение точек \(A\) и \(B\) можно определить, используя уравнения окружностей. Первая окружность описывается уравнением \((x — x_M)^2 + (y — y_M)^2 = 4^2\), вторая — \((x — x_P)^2 + (y — y_P)^2 = 5^2\), где \((x_M, y_M)\) и \((x_P, y_P)\) — координаты центров \(M\) и \(P\). Решая систему этих уравнений, находим координаты точек пересечения \(A\) и \(B\). Эти точки и будут искомыми, так как по условию они находятся на расстояниях 4 см и 5 см от центров \(M\) и \(P\) соответственно.