ГДЗ по Математике 5 Класс Часть 2 Номер 69 Мнемозина Виленкин, Жохов — Подробные Ответы

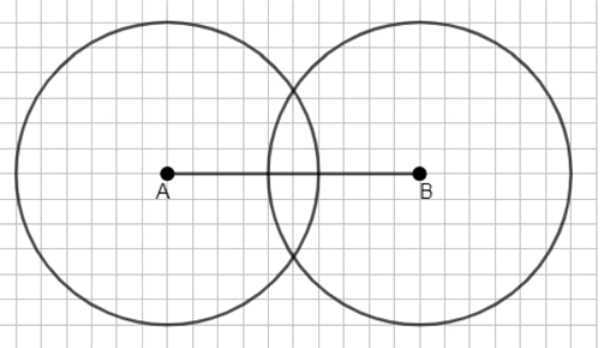
Отметьте точки \(A\) и \(B\) так, что \(AB = 5\) см. Проведите окружности одинакового радиуса с центрами \(A\) и \(B\) так, чтобы они:
а) пересекались в двух точках;
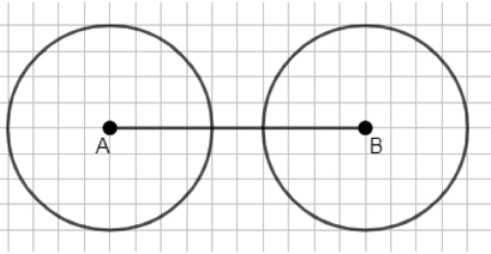
б) не имели общих точек.

а) Окружности пересекаются в двух точках, если расстояние между центрами \( A \) и \( B \) меньше суммы радиусов и больше их разности:
\( |AB| < r_A + r_B \) и \( |AB| > |r_A — r_B| \).

б) Окружности не имеют общих точек, если расстояние между центрами \( A \) и \( B \) больше суммы радиусов или меньше их разности:
\( |AB| > r_A + r_B \) или \( |AB| < |r_A — r_B| \).

а) Две окружности пересекаются в двух точках тогда, когда расстояние между их центрами \(A\) и \(B\) строго меньше суммы радиусов, но при этом больше абсолютной разности радиусов. Это условие можно записать так: \( |AB| < r_A + r_B \) и одновременно \( |AB| > |r_A — r_B| \). Здесь \(r_A\) и \(r_B\) — радиусы окружностей с центрами в точках \(A\) и \(B\) соответственно. Если расстояние между центрами слишком велико, окружности не смогут пересечься, потому что они будут слишком далеко друг от друга. Если же расстояние слишком мало, одна окружность может полностью лежать внутри другой без касания.

Условие \( |AB| < r_A + r_B \) означает, что центры окружностей расположены так, что их радиусы перекрываются, то есть окружности могут пересекаться или касаться. Но чтобы пересечение было именно в двух точках, расстояние не должно быть равно сумме радиусов (иначе окружности касаются в одной точке). Второе условие \( |AB| > |r_A — r_B| \) гарантирует, что одна окружность не находится полностью внутри другой без пересечений. Если расстояние между центрами меньше абсолютной разности радиусов, одна окружность лежит внутри другой и пересечений нет.

Таким образом, две окружности имеют ровно две точки пересечения, когда центры находятся на промежутке расстояний между суммой радиусов и их разностью. В этом случае две окружности частично накладываются, и у них есть две общие точки, где они пересекаются.

б) Окружности не имеют общих точек, если расстояние между их центрами \(A\) и \(B\) либо больше суммы радиусов, либо меньше абсолютной разности радиусов. Записывается это условие так: \( |AB| > r_A + r_B \) или \( |AB| < |r_A — r_B| \). В первом случае окружности расположены слишком далеко друг от друга и не пересекаются, так как радиусы не достигают друг до друга. Во втором случае одна окружность находится полностью внутри другой, но не касается её, так как расстояние между центрами слишком мало для касания. Если \( |AB| > r_A + r_B \), то расстояние между центрами превышает сумму радиусов, и окружности расположены отдельно, без точек пересечения. Это значит, что они не соприкасаются и не пересекаются, то есть множество общих точек пусто — \(\emptyset\).

Если же \( |AB| < |r_A — r_B| \), то одна окружность полностью вложена в другую, но так как расстояние между центрами меньше разности радиусов, они не касаются и не пересекаются. В этом случае также множество общих точек равно \(\emptyset\).

Таким образом, отсутствие общих точек у двух окружностей связано с тем, что либо они слишком далеко друг от друга, либо одна окружность находится внутри другой без касания. В обоих случаях пересечения нет.