ГДЗ по Математике 5 Класс Часть 2 Номер 649 Мнемозина Виленкин, Жохов — Подробные Ответы

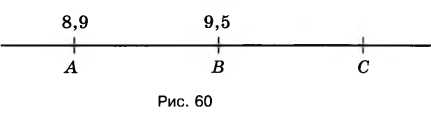
На рисунке 60 \(AB = BC\), где \(A(8,9)\) и \(B(9,5)\). Найдите координату точки \(C\). Чему равно среднее арифметическое координат точек \(A\) и \(C\)?

Так как точка \(C\) находится от точки \(B\) на расстоянии \(AB = 9,5 — 8,9 = 0,6\), то координата точки \(C\) равна: \(9,5 + 0,6 = 10,1\).

Среднее арифметическое координат точек \(A\) и \(C\) равно точке \(B\) с координатой \(9,5\): \((8,9 + 10,1) : 2 = 19 : 2 = 9,5\).

Так как точка \(C\) находится на расстоянии от точки \(B\), сначала нужно определить это расстояние. Из условия известно, что расстояние \(AB\) равно разности координат точек \(A\) и \(B\). Координата точки \(A\) равна \(9,5\), а координата точки \(B\) равна \(8,9\). Чтобы найти расстояние между ними, вычитаем координату \(B\) из координаты \(A\): \(9,5 — 8,9 = 0,6\). Это значит, что точка \(C\) находится на расстоянии \(0,6\) от точки \(B\).

Далее, чтобы найти координату точки \(C\), нужно прибавить это расстояние к координате точки \(B\), так как \(C\) лежит дальше по оси, чем \(B\). Таким образом, координата точки \(C\) равна сумме координаты \(B\) и расстояния: \(8,9 + 0,6 = 10,1\). Это значение и будет координатой точки \(C\).

Теперь проверим, что точка \(B\) действительно является средней между точками \(A\) и \(C\). Среднее арифметическое координат двух точек вычисляется как сумма их координат, делённая на 2. Координаты точек \(A\) и \(C\) равны \(8,9\) и \(10,1\) соответственно. Складываем их: \(8,9 + 10,1 = 19\). Делим сумму на 2: \(\frac{19}{2} = 9,5\). Полученное значение совпадает с координатой точки \(B\), что подтверждает, что \(B\) действительно средняя точка между \(A\) и \(C\).