ГДЗ по Математике 5 Класс Часть 2 Номер 6 Мнемозина Виленкин, Жохов — Подробные Ответы

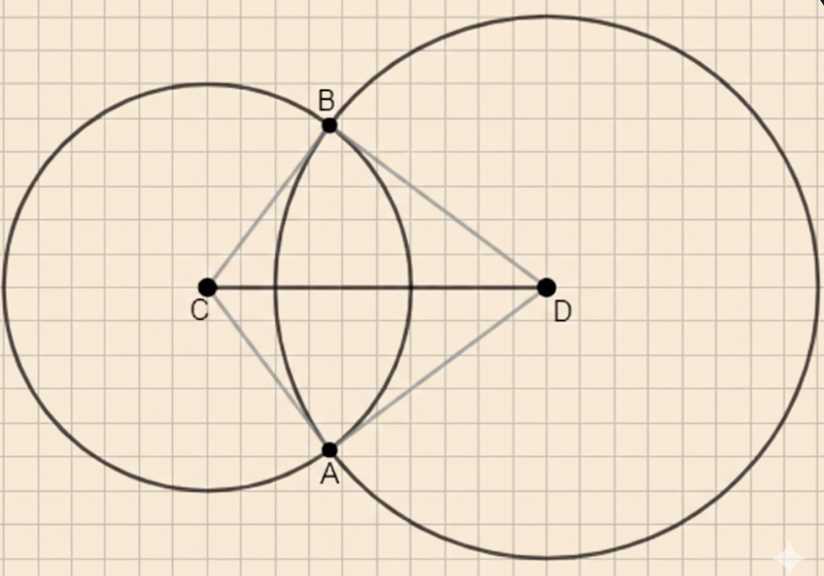
Начертите отрезок \(CD\), равный 5 см. Проведите окружность с центром \(C\) и радиусом 3 см, а также другую окружность с центром \(D\) и радиусом 4 см. Обозначьте точки пересечения окружностей буквами \(A\) и \(B\). Чему равны длины отрезков \(AC\), \(CB\), \(DA\) и \(BD\)?

Дано: \( AC = CB = r = 3 \, см \), \( DA = BD = r = 4 \, см \).

Треугольник \( \triangle ABC \) равнобедренный с основанием \( AB \).

Треугольник \( \triangle ABD \) равнобедренный с основанием \( AB \).

Так как \( AC = CB = 3 \) и \( DA = BD = 4 \), то \( AB = AC + CB = 6 \, см \).

Используем теорему Пифагора для треугольника \( \triangle ACD \):

Пусть \( CD = x \).

Тогда \( AD = 4 \), \( AC = 3 \), \( CD = x \).

В треугольнике \( \triangle ACD \):

\( AD^2 = AC^2 + CD^2 \)

\( 4^2 = 3^2 + x^2 \)

\( 16 = 9 + x^2 \)

\( x^2 = 7 \)

\( x = \sqrt{7} \, см \).

Расстояние между центрами окружностей \( C \) и \( D \) равно \( \sqrt{7} \).

Дано, что \( AC = CB = r = 3 \, см \), то есть точки \( A \) и \( B \) лежат на окружности с центром в точке \( C \) и радиусом 3 см. Это значит, что отрезки \( AC \) и \( CB \) равны, а сама точка \( C \) является центром окружности, проходящей через точки \( A \) и \( B \). Таким образом, длина отрезка \( AB \) равна сумме \( AC \) и \( CB \), то есть \( AB = AC + CB = 3 + 3 = 6 \, см \). Это важно, так как \( AB \) является общей хордой двух пересекающихся окружностей.

Далее известно, что \( DA = BD = r = 4 \, см \), то есть точка \( D \) является центром второй окружности, радиус которой равен 4 см, и эта окружность также проходит через точки \( A \) и \( B \). Отрезки \( DA \) и \( BD \) равны, значит треугольник \( ABD \) тоже равнобедренный с основанием \( AB = 6 \, см \). Теперь мы можем рассмотреть треугольник \( ACD \), где нам нужно найти расстояние между центрами окружностей \( C \) и \( D \), то есть длину отрезка \( CD \).

Для нахождения длины \( CD \) используем теорему Пифагора в прямоугольном треугольнике \( ACD \). Заметим, что \( AB \) — общая хорда, и поскольку \( AC = CB \), а \( DA = BD \), то эта хорда является общей для двух окружностей. Точки \( A \) и \( B \) лежат на обеих окружностях, а центры \( C \) и \( D \) находятся по разные стороны от хорды \( AB \). В треугольнике \( ACD \) известны стороны \( AC = 3 \, см \) и \( AD = 4 \, см \). Нам нужно найти \( CD \).

Применяем теорему Пифагора: \( AD^2 = AC^2 + CD^2 \), откуда \( CD^2 = AD^2 — AC^2 \). Подставляем значения: \( CD^2 = 4^2 — 3^2 = 16 — 9 = 7 \). Следовательно, \( CD = \sqrt{7} \, см \). Это и есть искомое расстояние между центрами окружностей. Таким образом, мы нашли длину отрезка \( CD \), используя свойства равнобедренных треугольников и теорему Пифагора.