ГДЗ по Математике 5 Класс Часть 2 Номер 588 Мнемозина Виленкин, Жохов — Подробные Ответы

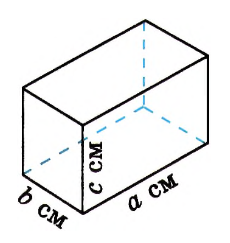
Длина прямоугольного параллелепипеда равна \(a\) см, ширина \(b\) см и высота \(c\) см. Найдите объём, площадь поверхности и сумму длин всех рёбер этого параллелепипеда, если:
а) \(a = 5,9\), \(b = 4\), \(c = 12\);
б) \(a = 14,1\), \(b = 8\), \(c = 2,5\);
в) \(a = 0,67\), \(b = 0,85\), \(c = 2,52\);
г) \(a = 2,07\), \(b = 0,95\), \(c = 4,24\).

\( V = abc; \quad S_{\text{поверх}} = 2(ab + bc + ac); \quad l = 4(a + b + c) \).

Сумма длин всех рёбер — \( l \).

а) Если \( a = 5{,}9 \, \text{см}; \quad b = 4 \, \text{см}; \quad c = 12 \, \text{см} \):

\( V = 5{,}9 \cdot 4 \cdot 12 = 5{,}9 \cdot 48 = 283{,}2 \, \text{см}^3 \).

\( S_{\text{поверх}} = 2 (5{,}9 \cdot 4 + 4 \cdot 12 + 5{,}9 \cdot 12) =\) \(= 2 (23{,}6 + 48 + 70{,}8) = 2 \cdot 142{,}4 = 284{,}8 \, \text{см}^2 \).

\( l = 4 (5{,}9 + 4 + 12) = 4 \cdot 21{,}9 = 87{,}6 \, \text{см} \).

Ответ: \( 283{,}2 \, \text{см}^3; \quad 284{,}8 \, \text{см}^2; \quad 87{,}6 \, \text{см} \).

б) Если \( a = 14{,}1 \, \text{см}; \quad b = 8 \, \text{см}; \quad c = 2{,}5 \, \text{см} \):

\( V = 14{,}1 \cdot 8 \cdot 2{,}5 = 14{,}1 \cdot 20 = 282 \, \text{см}^3 \).

\( S_{\text{поверх}} = 2 (14{,}1 \cdot 8 + 8 \cdot 2{,}5 + 14{,}1 \cdot 2{,}5) =\) \(= 2 (112{,}8 + 20 + 35{,}25) = 2 \cdot 168{,}05 = 336{,}1 \, \text{см}^2 \).

\( l = 4 (14{,}1 + 8 + 2{,}5) = 4 \cdot 24{,}6 =\) \(= 98{,}4 \, \text{см} \).

Ответ: \( 282 \, \text{см}^3; \quad 336{,}1 \, \text{см}^2; \quad 98{,}4 \, \text{см} \).

в) Если \(a = 0,67 \text{ см}\), \(b = 0,85 \text{ см}\), \(c = 2,52 \text{ см}\):

Объем \(V = a \cdot b \cdot c = 0,67 \cdot 0,85 \cdot 2,52 = 1,43514 \text{ см}^3\).

Площадь поверхности \(S_{\text{поверх}} = 2 \cdot (a b + b c + a c) =\) \(= 2 \cdot (0,5695 + 2,142 + 1,6884) = 2 \cdot 4,3999 = 8,7998 \text{ см}^2\).

Периметр \(l = 4 \cdot (a + b + c) = 4 \cdot (0,67 + 0,85 + 2,52) = 4 \cdot 4,04 = 16,16 \text{ см}\).

Ответ: \(1,43514 \text{ см}^3\); \(8,7998 \text{ см}^2\); \(16,16 \text{ см}\).

г) Если \(a = 2,07 \text{ см}\), \(b = 0,95 \text{ см}\), \(c = 4,24 \text{ см}\):

Объем \(V = a \cdot b \cdot c = 2,07 \cdot 0,95 \cdot 4,24 = 8,33796 \text{ см}^3\).

Площадь поверхности \(S_{\text{поверх}} = 2 \cdot (a b + b c + a c) =\) \(= 2 \cdot (1,9665 + 4,028 + 8,7768) = 2 \cdot 14,7713 = 29,5426 \text{ см}^2\).

Периметр \(l = 4 \cdot (a + b + c) = 4 \cdot (2,07 + 0,95 + 4,24) = 4 \cdot 7,26 = 29,04 \text{ см}\).

Ответ: \(8,33796 \text{ см}^3\); \(29,5426 \text{ см}^2\); \(29,04 \text{ см}\).

а) Для вычисления объёма прямоугольного параллелепипеда используется формула \( V = abc \), где \( a \), \( b \), \( c \) — длины трёх измерений. В данном случае \( a = 5{,}9 \, \text{см} \), \( b = 4 \, \text{см} \), \( c = 12 \, \text{см} \). Перемножая эти значения, получаем \( V = 5{,}9 \cdot 4 \cdot 12 = 5{,}9 \cdot 48 = 283{,}2 \, \text{см}^3 \). Это значение показывает, сколько кубических сантиметров занимает тело.

Площадь поверхности вычисляется по формуле \( S_{\text{поверх}} = 2(ab + bc + ac) \). Сначала считаем произведения пар сторон: \( ab = 5{,}9 \cdot 4 = 23{,}6 \), \( bc = 4 \cdot 12 = 48 \), \( ac = 5{,}9 \cdot 12 = 70{,}8 \). Складываем эти значения: \( 23{,}6 + 48 + 70{,}8 = 142{,}4 \). Умножаем на 2, так как у параллелепипеда две противоположные поверхности каждого вида: \( 2 \cdot 142{,}4 = 284{,}8 \, \text{см}^2 \).

Сумму длин всех рёбер находим по формуле \( l = 4(a + b + c) \), так как у параллелепипеда 12 рёбер, по четыре каждого размера. Складываем длины: \( 5{,}9 + 4 + 12 = 21{,}9 \), умножаем на 4: \( 4 \cdot 21{,}9 = 87{,}6 \, \text{см} \). Это сумма всех рёбер, измеренная в сантиметрах.

б) При других значениях сторон \( a = 14{,}1 \, \text{см} \), \( b = 8 \, \text{см} \), \( c = 2{,}5 \, \text{см} \) вычисляем объём по той же формуле: \( V = abc = 14{,}1 \cdot 8 \cdot 2{,}5 \). Сначала умножаем \( 8 \cdot 2{,}5 = 20 \), затем \( 14{,}1 \cdot 20 = 282 \, \text{см}^3 \). Это объём параллелепипеда.

Для площади поверхности считаем \( ab = 14{,}1 \cdot 8 = 112{,}8 \), \( bc = 8 \cdot 2{,}5 = 20 \), \( ac = 14{,}1 \cdot 2{,}5 = 35{,}25 \). Складываем: \( 112{,}8 + 20 + 35{,}25 = 168{,}05 \). Умножаем на 2, получаем \( 2 \cdot 168{,}05 = 336{,}1 \, \text{см}^2 \).

Сумма длин рёбер: \( l = 4(a + b + c) = 4(14{,}1 + 8 + 2{,}5) \). Складываем: \( 14{,}1 + 8 + 2{,}5 = 24{,}6 \), умножаем на 4: \( 4 \cdot 24{,}6 = 98{,}4 \, \text{см} \). Это итоговая длина всех рёбер.

в) Для вычисления объема прямоугольного параллелепипеда с ребрами \(a = 0,67 \text{ см}\), \(b = 0,85 \text{ см}\), \(c = 2,52 \text{ см}\) используется формула произведения трех измерений: \(V = a \cdot b \cdot c\). Сначала умножаем \(a\) на \(b\), получая \(0,67 \cdot 0,85 = 0,5695\). Затем результат умножаем на \(c\), то есть \(0,5695 \cdot 2,52 = 1,43514\). Таким образом, объем равен \(1,43514 \text{ см}^3\).

Площадь поверхности вычисляется по формуле \(S_{\text{поверх}} = 2 \cdot (a b + b c + a c)\). Сначала считаем произведения пар ребер: \(a b = 0,67 \cdot 0,85 = 0,5695\), \(b c = 0,85 \cdot 2,52 = 2,142\), \(a c = 0,67 \cdot 2,52 = 1,6884\). Складываем эти значения: \(0,5695 + 2,142 + 1,6884 = 4,3999\). Умножаем сумму на 2, получая \(8,7998 \text{ см}^2\).

Периметр по формуле \(l = 4 \cdot (a + b + c)\) равен \(4 \cdot (0,67 + 0,85 + 2,52) = 4 \cdot 4,04 = 16,16 \text{ см}\). Здесь сначала складываем длины всех ребер, так как периметр — это сумма всех сторон в основании, умноженная на 4 (четыре ребра). Результат показывает общую длину всех ребер.

г) Для другого параллелепипеда с измерениями \(a = 2,07 \text{ см}\), \(b = 0,95 \text{ см}\), \(c = 4,24 \text{ см}\) объем вычисляется аналогично: сначала перемножаем \(a\) и \(b\), получаем \(2,07 \cdot 0,95 = 1,9665\), затем результат умножаем на \(c\): \(1,9665 \cdot 4,24 = 8,33796 \text{ см}^3\).

Площадь поверхности рассчитывается по той же формуле: \(S_{\text{поверх}} = 2 \cdot (a b + b c + a c)\). Вычисляем каждое произведение: \(a b = 1,9665\), \(b c = 0,95 \cdot 4,24 = 4,028\), \(a c = 2,07 \cdot 4,24 = 8,7768\). Складываем: \(1,9665 + 4,028 + 8,7768 = 14,7713\). Умножаем на 2, получая \(29,5426 \text{ см}^2\).

Периметр вычисляется как сумма всех ребер, умноженная на 4: \(l = 4 \cdot (2,07 + 0,95 + 4,24) = 4 \cdot 7,26 = 29,04 \text{ см}\). Это показывает общую длину всех ребер параллелепипеда, что важно для расчета, например, длины материала для обрамления или окантовки.