
Учебник по математике для 5 класса «Мнемозина» авторов Виленкин и Жохов представляет собой качественное пособие, которое активно используется в школьной программе. Этот учебник сочетает в себе подробные теоретические материалы, интересные задачи и увлекательные примеры, что делает его полезным инструментом для формирования базовых знаний и навыков у школьников.
ГДЗ по Математике 5 Класс Часть 2 Номер 516 Мнемозина Виленкин, Жохов — Подробные Ответы
Подумайте, по какому правилу составлен ряд чисел, и запишите ещё два числа этого ряда:
а) Каждое следующее число больше предыдущего на 0,6:
\(1{,}2 + 0{,}6 = 1{,}8\), \(1{,}8 + 0{,}6 = 2{,}4\), \(2{,}4 + 0{,}6 = 3\), \(3 + 0{,}6 = 3{,}6\), \(3{,}6 + 0{,}6 = 4{,}2\).
Тогда:
\(1{,}2; 1{,}8; 2{,}4; 3; 3{,}6; 4{,}2 \ldots\)
б) Каждое следующее число меньше предыдущего на 0,7:
\(9{,}6 — 0{,}7 = 8{,}9\), \(8{,}9 — 0{,}7 = 8{,}2\), \(8{,}2 — 0{,}7 = 7{,}5\), \(7{,}5 — 0{,}7 = 6{,}8\), \(6{,}8 — 0{,}7 = 6{,}1\).
Тогда:
\(9{,}6; 8{,}9; 8{,}2; 7{,}5; 6{,}8; 6{,}1 \ldots\)
в) Каждое следующее число больше предыдущего в 2 раза:
\(0{,}9 \cdot 2 = 1{,}8\), \(1{,}8 \cdot 2 = 3{,}6\), \(3{,}6 \cdot 2 = 7{,}2\), \(7{,}2 \cdot 2 = 14{,}4\), \(14{,}4 \cdot 2 = 28{,}8\).
Тогда:
\(0{,}9; 1{,}8; 3{,}6; 7{,}2; 14{,}4; 28{,}8 \ldots\)
г) Каждое следующее число на нечётном месте больше предыдущего на 1, а на чётном месте — на 0,7:
Нечётные: \(1{,}2 + 1 = 2{,}2\), \(2{,}2 + 1 = 3{,}2\), \(3{,}2 + 1 = 4{,}2\)
Чётные: \(0{,}7 + 0{,}7 = 1{,}4\), \(1{,}4 + 0{,}7 = 2{,}1\), \(2{,}1 + 0{,}7 = 2{,}8\)
Тогда:
\(1{,}2; 0{,}7; 2{,}2; 1{,}4; 3{,}2; 2{,}1; 4{,}2; 2{,}8 \ldots\)
а) В этом задании нам дано, что каждое следующее число в последовательности больше предыдущего на 0,6. Это означает, что мы имеем арифметическую прогрессию с разностью \(d = 0{,}6\). Начальное число равно \(1{,}2\). Чтобы найти последующие члены, нужно к каждому предыдущему прибавлять 0,6. Например, первое число \(1{,}2\), следующее будет \(1{,}2 + 0{,}6 = 1{,}8\). Далее к \(1{,}8\) прибавляем 0,6 и получаем \(2{,}4\), затем \(2{,}4 + 0{,}6 = 3\), и так далее.
Таким образом, последовательность строится по правилу \(a_{n+1} = a_n + 0{,}6\), где \(a_1 = 1{,}2\). Продолжая вычисления, получаем члены: \(3 + 0{,}6 = 3{,}6\), \(3{,}6 + 0{,}6 = 4{,}2\). Итоговая последовательность: \(1{,}2; 1{,}8; 2{,}4; 3; 3{,}6; 4{,}2 \ldots\).
б) Здесь каждое следующее число меньше предыдущего на 0,7. Это тоже арифметическая прогрессия, но с отрицательной разностью \(d = -0{,}7\). Начальное число равно \(9{,}6\). Для нахождения следующего числа нужно отнять 0,7 от предыдущего. Например, \(9{,}6 — 0{,}7 = 8{,}9\), затем \(8{,}9 — 0{,}7 = 8{,}2\), и так далее.
Правило для последовательности: \(a_{n+1} = a_n — 0{,}7\), где \(a_1 = 9{,}6\). Продолжая вычисления: \(8{,}2 — 0{,}7 = 7{,}5\), \(7{,}5 — 0{,}7 = 6{,}8\), \(6{,}8 — 0{,}7 = 6{,}1\). Последовательность: \(9{,}6; 8{,}9; 8{,}2; 7{,}5; 6{,}8; 6{,}1 \ldots\).
в) В этом случае каждое следующее число в последовательности больше предыдущего в 2 раза. Это геометрическая прогрессия с знаменателем \(q = 2\) и начальным членом \(a_1 = 0{,}9\). Чтобы найти следующий член, нужно умножить предыдущий на 2. Например, \(0{,}9 \cdot 2 = 1{,}8\), \(1{,}8 \cdot 2 = 3{,}6\), \(3{,}6 \cdot 2 = 7{,}2\), и так далее.
Правило: \(a_{n+1} = a_n \cdot 2\), где \(a_1 = 0{,}9\). Продолжаем: \(7{,}2 \cdot 2 = 14{,}4\), \(14{,}4 \cdot 2 = 28{,}8\). Последовательность: \(0{,}9; 1{,}8; 3{,}6; 7{,}2; 14{,}4; 28{,}8 \ldots\).
г) В этом задании последовательность строится по сложному правилу: числа на нечётных местах увеличиваются на 1 по сравнению с предыдущим числом на нечётной позиции, а числа на чётных местах увеличиваются на 0,7 по сравнению с предыдущим числом на чётной позиции. Начальные значения: первое число \(1{,}2\) (нечётное место), второе число \(0{,}7\) (чётное место).
Для чисел на нечётных местах: начиная с \(1{,}2\), прибавляем 1, получаем \(2{,}2\), затем \(2{,}2 + 1 = 3{,}2\), и \(3{,}2 + 1 = 4{,}2\). Для чисел на чётных местах: начиная с \(0{,}7\), прибавляем 0,7, получаем \(1{,}4\), затем \(1{,}4 + 0{,}7 = 2{,}1\), и \(2{,}1 + 0{,}7 = 2{,}8\).
Последовательность получается чередующейся: на нечётных позициях \(1{,}2; 2{,}2; 3{,}2; 4{,}2\), на чётных \(0{,}7; 1{,}4; 2{,}1; 2{,}8\). Итог: \(1{,}2; 0{,}7; 2{,}2; 1{,}4; 3{,}2; 2{,}1; 4{,}2; 2{,}8 \ldots\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


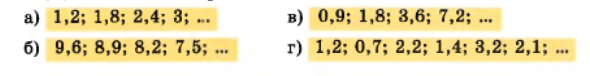



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!