ГДЗ по Математике 5 Класс Часть 2 Номер 5 Мнемозина Виленкин, Жохов — Подробные Ответы

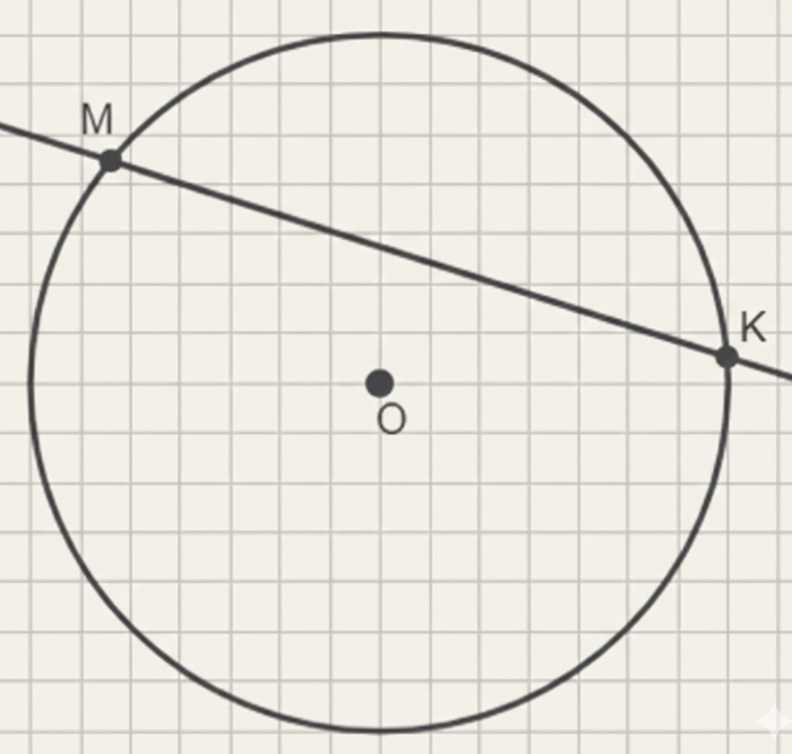
Начертите окружность с центром в точке \(O\) и радиусом 3 см 5 мм. Проведите прямую, которая пересекает окружность в точках \(M\) и \(K\). На каком расстоянии от центра окружности находятся эти точки?

Точки \( M \) и \( K \) лежат на окружности, значит расстояние от центра \( O \) до каждой из них равно радиусу окружности.

Расстояние \( OM = OK = 3 \text{ см } 5 \text{ мм} = 3{,}5 \text{ см} \).

Таким образом, радиус окружности равен \( 3{,}5 \text{ см} \).

Точки \( M \) и \( K \) лежат на окружности, что означает, что расстояние от центра окружности \( O \) до каждой из этих точек равно радиусу окружности. В геометрии радиус — это отрезок, соединяющий центр окружности с любой точкой на окружности. Поскольку обе точки лежат на окружности, расстояния \( OM \) и \( OK \) одинаковы и равны радиусу.

На рисунке видно, что расстояние от центра \( O \) до точек \( M \) и \( K \) составляет 3 см 5 мм. Для удобства вычислений нужно перевести миллиметры в сантиметры, так как единицы измерения должны совпадать. Мы знаем, что 10 мм равны 1 см, значит 5 мм — это \( \frac{5}{10} = 0{,}5 \) см. Следовательно, общее расстояние от центра до точки \( M \) или \( K \) равно \( 3 + 0{,}5 = 3{,}5 \) см.

Таким образом, радиус окружности равен \( 3{,}5 \) см. Это значение является ключевым для решения задач, связанных с этой окружностью, так как любые точки, лежащие на ней, находятся на одинаковом расстоянии от центра. В дальнейшем при вычислениях или построениях можно использовать именно этот радиус, что упрощает решение геометрических задач, связанных с данной окружностью.