ГДЗ по Математике 5 Класс Часть 2 Номер 474 Мнемозина Виленкин, Жохов — Подробные Ответы

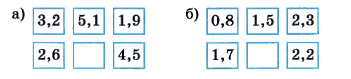
Найдите пропущенное число:

а) \(3,2 + 1,9 = 5,1\) — сумма крайних чисел равна среднему числу.
Значит:
\(2,6 + 4,5 = 7,1\) — среднее число.

б) \(2,3 — 0,8 = 1,5\) — разность правого крайнего числа и левого крайнего числа равна среднему числу.
Значит:
\(2,2 — 1,7 = 0,5\) — среднее число.

а) В этом пункте рассматривается ситуация, когда сумма крайних чисел равна среднему числу. Дано, что \(3,2 + 1,9 = 5,1\). Здесь «крайние числа» — это первое и третье число, а «среднее число» — второе. Проверка показывает, что сумма крайних чисел действительно равна среднему числу, то есть \(5,1\). Это условие позволяет понять, как найти среднее число в другом наборе чисел.

Теперь, используя это правило, смотрим на другой набор чисел: \(2,6\) и \(4,5\). Чтобы найти среднее число, мы складываем крайние числа: \(2,6 + 4,5 = 7,1\). Следовательно, среднее число в этом случае будет равно \(7,1\), так как по условию сумма крайних чисел должна быть равна среднему числу.

б) Во втором пункте рассматривается другой вид зависимости между числами — разность правого крайнего числа и левого крайнего числа равна среднему числу. Из условия видно, что \(2,3 — 0,8 = 1,5\). Здесь крайние числа — \(2,3\) (правое) и \(0,8\) (левое), а среднее число — \(1,5\). Это значит, что если вычесть левое число из правого, результат будет равен среднему числу.

Используя это правило для другого набора чисел, берём \(2,2\) и \(1,7\). Вычитаем: \(2,2 — 1,7 = 0,5\). Следовательно, среднее число в этом случае равно \(0,5\), так как оно должно быть равно разности крайних чисел. Таким образом, мы применили правило, что разность крайних чисел равна среднему числу, чтобы найти среднее число в новом примере.