ГДЗ по Математике 5 Класс Часть 2 Номер 470 Мнемозина Виленкин, Жохов — Подробные Ответы

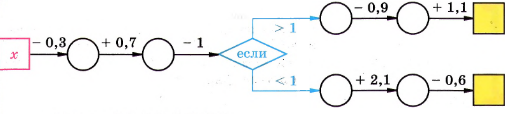
Восстановите цепочку вычислений:

Если \( x = 0,8 \);
\( 0,8 — 0,3 = 0,5 \);
\( 0,5 + 0,7 = 1,2 \);
\( 1,2 — 1 = 0,2 < 1 \);
\( 0,2 + 2,1 = 2,3 \);
\( 2,3 — 0,6 = 1,7 \).

Если \( x = 1,3 \);
\( 1,3 — 0,3 = 1 \);
\( 1 + 0,7 = 1,7 \);
\( 1,7 — 1 = 0,7 < 1 \);
\( 0,7 + 2,1 = 2,8 \);
\( 2,8 — 0,6 = 2,2 \).

Если \( x = 1,8 \);
\( 1,8 — 0,3 = 1,5 \);
\( 1,5 + 0,7 = 2,2 \);
\( 2,2 — 1 = 1,2 > 1 \);
\( 1,2 — 0,9 = 0,3 \);
\( 0,3 + 1,1 = 1,4 \).

Если \( x = 2,3 \);
\( 2,3 — 0,3 = 2 \);
\( 2 + 0,7 = 2,7 \);
\( 2,7 — 1 = 1,7 > 1 \);
\( 1,7 — 0,9 = 0,8 \);
\( 0,8 + 1,1 = 1,9 \).

а) Если \( x = 0,8 \), первым действием является вычитание \( 0,3 \) из \( 0,8 \). Это простая арифметическая операция, которая показывает, на сколько уменьшается значение \( x \). Получаем \( 0,8 — 0,3 = 0,5 \). Далее мы прибавляем к результату \( 0,7 \), что позволяет нам увеличить значение на указанную величину: \( 0,5 + 0,7 = 1,2 \). Следующий шаг — вычесть из полученного результата 1, чтобы проверить, насколько новое значение отличается от единицы: \( 1,2 — 1 = 0,2 \). Здесь важно отметить, что \( 0,2 < 1 \), что указывает на то, что результат меньше единицы. После этого прибавляем к \( 0,2 \) число \( 2,1 \), что даёт \( 0,2 + 2,1 = 2,3 \). Последним действием в этом блоке является вычитание \( 0,6 \) из \( 2,3 \), что приводит к значению \( 2,3 — 0,6 = 1,7 \).

б) При \( x = 1,3 \) сначала вычитаем \( 0,3 \), чтобы увидеть разницу с исходным значением: \( 1,3 — 0,3 = 1 \). Это ровно единица, что важно для последующих вычислений. Затем прибавляем \( 0,7 \), получая \( 1 + 0,7 = 1,7 \). Следующий шаг — вычитание 1 из результата, чтобы проверить, насколько значение превышает или меньше единицы: \( 1,7 — 1 = 0,7 \), и так как \( 0,7 < 1 \), это указывает, что результат меньше единицы. После этого прибавляем \( 2,1 \), что даёт \( 0,7 + 2,1 = 2,8 \). В конце вычитаем \( 0,6 \) из \( 2,8 \) и получаем \( 2,8 — 0,6 = 2,2 \).

в) При \( x = 1,8 \) сначала вычитаем \( 0,3 \), чтобы понять, насколько уменьшилось значение: \( 1,8 — 0,3 = 1,5 \). Затем прибавляем \( 0,7 \), что даёт \( 1,5 + 0,7 = 2,2 \). Следующий шаг — вычесть 1 из результата, чтобы определить, насколько значение превышает единицу: \( 2,2 — 1 = 1,2 \), и поскольку \( 1,2 > 1 \), это означает, что значение больше единицы. После этого вычитаем \( 0,9 \), получая \( 1,2 — 0,9 = 0,3 \). В заключение прибавляем \( 1,1 \), что даёт итоговое значение \( 0,3 + 1,1 = 1,4 \).

г) При \( x = 2,3 \) сначала вычитаем \( 0,3 \), чтобы получить разницу: \( 2,3 — 0,3 = 2 \). Затем прибавляем \( 0,7 \), что приводит к \( 2 + 0,7 = 2,7 \). Следующий шаг — вычесть 1 из результата, чтобы проверить превышение единицы: \( 2,7 — 1 = 1,7 \), где \( 1,7 > 1 \), что означает, что значение больше единицы. После этого вычитаем \( 0,9 \), получая \( 1,7 — 0,9 = 0,8 \). В конце прибавляем \( 1,1 \), что даёт итоговое значение \( 0,8 + 1,1 = 1,9 \).