ГДЗ по Математике 5 Класс Часть 2 Номер 467 Мнемозина Виленкин, Жохов — Подробные Ответы

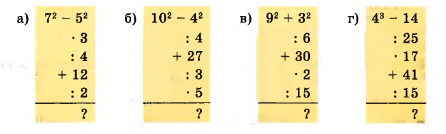
Вычислите устно:

а) \(7^2 — 5^2 = 49 — 25 = 24;\)
\(24 \cdot 3 = 72;\)
\(72 : 4 = 18;\)
\(18 + 12 = 30;\)
\(30 : 2 = 15.\)

б) \(10^2 — 4^2 = 100 — 16 = 84;\)
\(84 : 4 = 21;\)
\(21 + 27 = 48;\)
\(48 : 3 = 16;\)
\(16 \cdot 5 = 80.\)

в) \(9^2 + 3^2 = 81 + 9 = 90;\)
\(90 : 6 = 15;\)
\(15 + 30 = 45;\)
\(45 \cdot 2 = 90;\)
\(90 : 15 = 6.\)

г) \(4^3 — 14 = 64 — 14 = 50;\)
\(50 : 25 = 2;\)
\(2 \cdot 17 = 34;\)
\(34 + 41 = 75;\)
\(75 : 15 = 5.\)

а) Начинаем с вычисления разности квадратов: возводим в квадрат числа 7 и 5, получаем \(7^2 = 49\) и \(5^2 = 25\). Затем вычитаем: \(49 — 25 = 24\). Это базовое действие с квадратами чисел, которое часто используется для упрощения выражений. Далее умножаем полученный результат на 3: \(24 \cdot 3 = 72\). Умножение здесь служит для увеличения значения в три раза, что соответствует условию задачи. После этого делим результат на 4: \(72 : 4 = 18\), что уменьшает число в 4 раза, показывая, как меняется величина при делении.

Следующий шаг — сложение: к числу 18 прибавляем 12, получая \(18 + 12 = 30\). Это простое арифметическое действие, показывающее, как комбинируются разные операции в одной последовательности. В конце делим 30 на 2: \(30 : 2 = 15\), что завершает цепочку вычислений и даёт итоговый ответ. Таким образом, последовательно выполняя операции, мы переходим от исходного выражения к конечному результату.

б) В этом примере также начинаем с вычисления разности квадратов: \(10^2 = 100\) и \(4^2 = 16\), затем вычитаем \(100 — 16 = 84\). Это классическая формула разности квадратов, которая часто используется для упрощения выражений в алгебре. Далее делим полученное число на 4: \(84 : 4 = 21\), что уменьшает величину в четыре раза. После деления выполняем сложение: \(21 + 27 = 48\), прибавляя к результату новое число.

Дальше делим 48 на 3: \(48 : 3 = 16\), уменьшая число в три раза, и в конце умножаем 16 на 5: \(16 \cdot 5 = 80\), что увеличивает результат в пять раз. Такая последовательность действий показывает, как можно комбинировать разные арифметические операции для получения конечного значения, следуя строгому порядку вычислений.

в) Сначала вычисляем сумму квадратов: \(9^2 = 81\) и \(3^2 = 9\), складываем их: \(81 + 9 = 90\). Это действие отличается от предыдущих, так как здесь используется сумма квадратов, а не разность. Следующим шагом делим 90 на 6: \(90 : 6 = 15\), что уменьшает число в шесть раз. Затем прибавляем 30 к результату: \(15 + 30 = 45\), увеличивая величину.

После этого умножаем 45 на 2: \(45 \cdot 2 = 90\), удваивая число, и в конце делим 90 на 15: \(90 : 15 = 6\), что уменьшает число в пятнадцать раз. Такая цепочка операций иллюстрирует, как можно комбинировать сложение, умножение и деление для достижения нужного результата.

г) Начинаем с вычисления разности: \(4^3 = 64\), отнимаем 14, получая \(64 — 14 = 50\). Здесь используется куб числа 4, что показывает работу с более сложными степенями. Затем делим 50 на 25: \(50 : 25 = 2\), уменьшая число в 25 раз. Следующим действием умножаем 2 на 17: \(2 \cdot 17 = 34\), увеличивая результат.

Потом прибавляем 41: \(34 + 41 = 75\), увеличивая величину за счёт сложения, и в конце делим 75 на 15: \(75 : 15 = 5\), что уменьшает число в 15 раз. Эта последовательность демонстрирует, как различные арифметические операции и степени могут сочетаться для получения итогового значения.