
Учебник по математике для 5 класса «Мнемозина» авторов Виленкин и Жохов представляет собой качественное пособие, которое активно используется в школьной программе. Этот учебник сочетает в себе подробные теоретические материалы, интересные задачи и увлекательные примеры, что делает его полезным инструментом для формирования базовых знаний и навыков у школьников.
ГДЗ по Математике 5 Класс Часть 2 Номер 455 Мнемозина Виленкин, Жохов — Подробные Ответы
Поставьте вместо звёздочек пропущенные цифры:
а) Складываем единицы: \(5 + 2 = 7\). Тогда, \(* = 7\).
Складываем десятки: \(8 + 8 = 16\). Тогда, \(* = 6\).
Складываем сотни, один был в уме: \(1 + 7 + 9 = 17\). Тогда, \(* = 9\).
Складываем единицы тысяч, один был в уме: \(1 + 1 + 4 = 6\). Тогда, \(* = 1\).
Складываем десятки тысяч: \(3 + 0 = 3\). Тогда, \(* = 0\).
Складываем сотни тысяч: \(6 + 3 = 9\). Тогда, \(* = 6\).
Переписываем цифру 6. Тогда, \(* = 6\).
б) Складываем единицы: \(8 + 5 = 13\). Тогда, \(* = 8\).
Складываем десятки, один был в уме: \(1 + 3 + 5 = 9\). Тогда, \(* = 5\).
Складываем сотни: \(4 + 2 = 6\). Тогда, \(* = 6\).
Складываем единицы тысяч: \(7 + 9 = 16\). Тогда, \(* = 9\).
Складываем десятки тысяч, один был в уме: \(1 + 5 + 4 = 10\). Тогда, \(* = 5\).
Складываем сотни тысяч, один был в уме: \(1 + 7 + 3 = 11\). Тогда, \(* = 3\).
Складываем единицы миллионов, один был в уме: \(1 + 3 + 4 = 8\). Тогда, \(* = 8\).
а) При сложении чисел поразрядно важно учитывать переносы, которые возникают, когда сумма цифр в одном разряде превышает 9. Сначала складываем единицы: \(5 + 2 = 7\). Поскольку сумма меньше 10, перенос в следующий разряд отсутствует, и цифра результата равна 7. Далее складываем десятки: \(8 + 8 = 16\). Поскольку сумма больше 9, в разряде десятков записываем 6, а 1 переносим в разряд сотен. В разряде сотен учитываем этот перенос и складываем: \(1 + 7 + 9 = 17\). Записываем 7, а 1 переносим в следующий разряд.
В разряде тысяч складываем с учётом переноса: \(1 + 1 + 4 = 6\). Здесь сумма меньше 10, перенос отсутствует, цифра результата — 6. Затем складываем десятки тысяч: \(3 + 0 = 3\), без переноса. В разряде сотен тысяч сумма: \(6 + 3 = 9\), также без переноса. Последняя цифра переписывается без изменений — 6. Таким образом, при сложении поразрядно важно учитывать переносы, чтобы правильно определить цифры результата.
б) При сложении единиц сначала складываем цифры: \(8 + 5 = 13\). Поскольку сумма превышает 9, в разряде единиц результат равен 3, а 1 переносим в разряд десятков. В разряде десятков учитываем перенос и складываем: \(1 + 3 + 5 = 9\). Здесь сумма равна 9, без дополнительного переноса, цифра результата — 9. При сложении сотен: \(4 + 2 = 6\), без переноса.
В разряде тысяч складываем: \(7 + 9 = 16\), из чего 6 записываем в разряд, а 1 переносим. В десятках тысяч с учётом переноса: \(1 + 5 + 4 = 10\), цифра результата 0, перенос 1 в сотни тысяч. В сотнях тысяч: \(1 + 7 + 3 = 11\), записываем 1, перенос 1 в миллионы. В миллионах: \(1 + 3 + 4 = 8\), цифра результата 8, без переноса.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


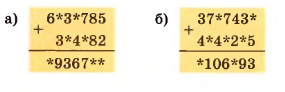



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!