ГДЗ по Математике 5 Класс Часть 2 Номер 449 Мнемозина Виленкин, Жохов — Подробные Ответы

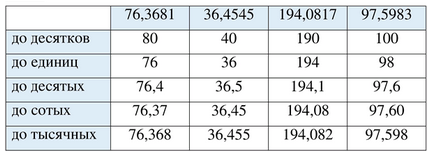
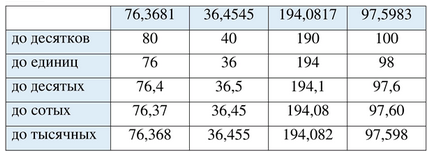
Округлите числа.

Для округления чисел до различных разрядов необходимо понять, как работает процесс округления. В исходных числах есть несколько знаков после запятой, и для каждого разряда мы определяем, какую цифру оставляем, а какую отбрасываем, учитывая правило округления.

Когда мы округляем число до десятков, мы смотрим на цифру в разряде единиц. Если она 5 или больше, то цифра в разряде десятков увеличивается на 1, иначе остаётся без изменений, а все цифры справа заменяются на нули. Например, для числа 76,3681 разряд десятков — это 7 (семьдесят), а цифра единиц — 6, которая больше 5, поэтому десятки округляются до 80.

При округлении до единиц мы смотрим на цифру в десятых. Если десятые 5 или больше, то единицы увеличиваются на 1, иначе остаются. Все цифры после единиц отбрасываются. В числе 36,4545 цифра единиц 6, а десятые 4, что меньше 5, значит округляем до 36.

Округление до десятых требует посмотреть на цифру в сотых. Если она 5 или больше, десятые увеличиваются на 1, иначе остаются. В числе 194,0817 сотые — 1, меньше 5, поэтому десятые остаются 0, и число округляется до 194,1.

Для округления до сотых смотрим на тысячные. Если тысячные 5 или больше, сотые увеличиваются на 1, иначе остаются. В числе 97,5983 тысячные 8, больше 5, значит сотые увеличиваются с 9 до 10, что приводит к увеличению десятых на 1 и сотых до 0, в итоге округление даёт 97,60.

Для тысячных просто отбрасываем все цифры после третьего знака после запятой без изменения, так как это самый мелкий разряд, который мы учитываем. Например, число 76,3681 при округлении до тысячных становится 76,368.