ГДЗ по Математике 5 Класс Часть 2 Номер 437 Мнемозина Виленкин, Жохов — Подробные Ответы

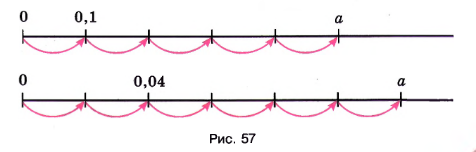
Используя рисунок 57, найдите число \(a\):

а) \( a = 0{,}1 + 0{,}1 + 0{,}1 + 0{,}1 + 0{,}1 = 0{,}5 \).

б) \( a = 0{,}04 + 0{,}04 + 0{,}04 = 0{,}08 + 0{,}04 = 0{,}12 \).

а) В данном примере нужно сложить пять одинаковых чисел \(0{,}1\). Каждое слагаемое равно \(0{,}1\), и мы складываем их последовательно: \(0{,}1 + 0{,}1 + 0{,}1 + 0{,}1 + 0{,}1\). Сложение одинаковых чисел можно заменить умножением этого числа на количество слагаемых, то есть \(0{,}1 \times 5\). Это упрощает вычисление и показывает, что сумма равна \(0{,}5\).

Таким образом, результат выражения можно получить двумя способами: либо сложить числа по отдельности, либо умножить число \(0{,}1\) на 5. В обоих случаях итоговый ответ будет одинаковым — \(a = 0{,}5\). Это демонстрирует простое свойство арифметики, когда сумма одинаковых слагаемых равна произведению одного слагаемого на их количество.

б) Во второй части задачи нужно сложить три числа: \(0{,}04 + 0{,}04 + 0{,}04\). Сначала складываем первые два числа: \(0{,}04 + 0{,}04 = 0{,}08\). Затем к полученной сумме прибавляем оставшееся число \(0{,}04\), получая итог: \(0{,}08 + 0{,}04 = 0{,}12\). Аналогично первому примеру, можно заметить, что три одинаковых числа \(0{,}04\) можно сложить, умножив \(0{,}04\) на 3, что также даст \(0{,}12\).

Такой подход упрощает вычисления и помогает понять, что сложение одинаковых дробных чисел эквивалентно умножению одного из них на количество слагаемых. В итоге получаем \(a = 0{,}12\), что соответствует сумме трех чисел по \(0{,}04\) каждое.