ГДЗ по Математике 5 Класс Часть 2 Номер 43 Мнемозина Виленкин, Жохов — Подробные Ответы

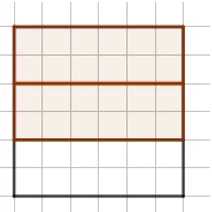
Начертите квадрат со стороной 6 клеток. Разделите его на 3 доли и закрасьте \(\frac{2}{3}\) квадрата. Какая часть квадрата осталась незакрашенной?

Осталась незакрашенной часть квадрата, равная \( \frac{1}{3} \).

Объяснение:

В квадрате три равные части, две из них закрашены, значит незакрашенная часть — одна треть.
Ответ: \( \frac{1}{3} \).

В квадрате изображено три равные горизонтальные полосы, образующие вместе весь квадрат. Две из этих полос закрашены коричневым цветом, а одна — нет. Поскольку площадь всего квадрата равна 1 (целому квадрату), каждая из трёх полос составляет равную часть площади квадрата. Это связано с тем, что полосы одинаковой высоты и ширины, то есть равны по площади. Следовательно, площадь каждой полосы равна \( \frac{1}{3} \) от площади всего квадрата.

Чтобы найти незакрашенную часть, нужно определить, какую долю от общего квадрата занимает незакрашенная полоса. Поскольку только одна из трёх полос не закрашена, её площадь и есть незакрашенная часть. Таким образом, незакрашенная часть равна \( \frac{1}{3} \) площади всего квадрата. Это можно записать как отношение площади незакрашенной полосы к площади всего квадрата: \( \frac{\text{площадь незакрашенной полосы}}{\text{площадь квадрата}} = \frac{1}{3} \).

В итоге, ответ получается простым и логичным: незакрашенная часть квадрата равна \( \frac{1}{3} \). Это значит, что две трети площади квадрата заняты закрашенными полосами, а одна треть остаётся незакрашенной. Такой подход помогает наглядно и точно определить долю незакрашенной части без необходимости измерять конкретные длины или площади, достаточно лишь понять, что квадрат разделён на три равные части.