ГДЗ по Математике 5 Класс Часть 2 Номер 429 Мнемозина Виленкин, Жохов — Подробные Ответы

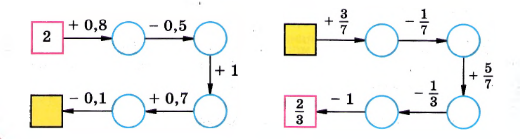
Восстановите цепочку вычислений:

1) \(2 + 0,8 = 2,8; \quad 2,8 — 0,5 = 2,3; \quad 2,3 + 1 = 3,3; \) \( \quad 3,3 + 0,7 = 4; \quad 4 — 0,1 = 3,9.\)

Тогда:
\(2 + 0,8 = 2,8 — 0,5 = 2,3 + 1 = 3,3 + 0,7 = 4 — 0,1 = 3,9.\)

2) Обратные действия:
\(\frac{2}{3} + 1 = 1 \frac{2}{3};\)
\(1 \frac{2}{3} + \frac{1}{3} = 2;\)
\(2 — \frac{5}{7} = 1 \frac{7}{7} — \frac{5}{7} = 1 \frac{2}{7};\)
\(1 \frac{2}{7} + \frac{1}{7} = 1 \frac{3}{7};\)
\(1 \frac{3}{7} — \frac{3}{7} = 1.\)

Тогда:
\(1 + \frac{3}{7} = 1 \frac{3}{7}; \quad 1 \frac{3}{7} — \frac{1}{7} = 1 \frac{2}{7}; \quad 1 \frac{2}{7} + \frac{5}{7} = 2; \quad 2 — \frac{1}{3} = 1 \frac{2}{3}; \quad 1 \frac{2}{3} — 1 = \frac{2}{3}.\)

1) Рассмотрим последовательность действий с десятичными числами. Сначала складываем \(2\) и \(0,8\). При сложении целого числа и десятичной дроби результат будет десятичной дробью, поэтому \(2 + 0,8 = 2,8\). Далее из полученного результата вычитаем \(0,5\). Вычитание десятичных дробей происходит по разрядам, как и сложение, поэтому \(2,8 — 0,5 = 2,3\). Следующий шаг — прибавляем к \(2,3\) число \(1\), что даёт \(3,3\). После этого прибавляем \(0,7\) к \(3,3\), получая \(4\). Наконец, вычитаем из \(4\) число \(0,1\), что даёт \(3,9\). Таким образом, каждое действие — это простое сложение или вычитание десятичных дробей, где важно правильно расположить запятую и соблюдать порядок операций.

В итоге все операции можно записать в одну цепочку: \(2 + 0,8 = 2,8 — 0,5 = 2,3 + 1 = 3,3 + 0,7 = 4 — 0,1 = 3,9\). Это показывает, что последовательное выполнение действий даёт конечный результат \(3,9\). Каждое промежуточное значение служит основой для следующего действия, что важно при решении подобных задач.

2) Рассмотрим обратные действия с дробями. Начинаем с суммы \(\frac{2}{3} + 1\). Чтобы сложить дробь с целым числом, целое число представляем в виде дроби с тем же знаменателем: \(1 = \frac{3}{3}\). Тогда сумма равна \(\frac{2}{3} + \frac{3}{3} = \frac{5}{3} = 1 \frac{2}{3}\). Следующий шаг — прибавить к \(1 \frac{2}{3}\) ещё \(\frac{1}{3}\), что даёт \(1 \frac{3}{3} = 2\), так как \(\frac{2}{3} + \frac{1}{3} = \frac{3}{3} = 1\).

Далее вычитаем из \(2\) дробь \(\frac{5}{7}\). Представим \(2\) в виде дроби с знаменателем \(7\): \(2 = \frac{14}{7}\). Тогда \(2 — \frac{5}{7} = \frac{14}{7} — \frac{5}{7} = \frac{9}{7} = 1 \frac{2}{7}\). К этому результату прибавляем \(\frac{1}{7}\), получая \(1 \frac{3}{7}\). Наконец, вычитаем \(\frac{3}{7}\) из \(1 \frac{3}{7}\), что даёт ровно \(1\), так как \(\frac{3}{7} — \frac{3}{7} = 0\).

Таким образом, обратные действия — это операции сложения и вычитания дробей, где важно привести дроби к общему знаменателю и правильно преобразовать смешанные числа. Это позволяет увидеть, как исходные значения восстанавливаются через последовательность обратных операций.

3) В заключение рассмотрим цепочку действий с дробями. Начинаем с суммы \(1 + \frac{3}{7}\), что даёт смешанное число \(1 \frac{3}{7}\). Затем вычитаем из него \(\frac{1}{7}\), что даёт \(1 \frac{2}{7}\), так как \( \frac{3}{7} — \frac{1}{7} = \frac{2}{7}\). Далее прибавляем \(\frac{5}{7}\), получая \(2\), поскольку \(\frac{2}{7} + \frac{5}{7} = \frac{7}{7} = 1\), а \(1 + 1 = 2\).

После этого из \(2\) вычитаем \(\frac{1}{3}\). Для этого представляем \(2\) как дробь с знаменателем \(3\): \(2 = \frac{6}{3}\). Тогда \(2 — \frac{1}{3} = \frac{6}{3} — \frac{1}{3} = \frac{5}{3} = 1 \frac{2}{3}\). И наконец, вычитаем \(1\), что даёт \(\frac{2}{3}\), потому что \(1 \frac{2}{3} — 1 = \frac{2}{3}\).

Эта последовательность показывает, как с помощью сложения и вычитания дробей можно получить нужный результат, используя приведение к общему знаменателю и преобразование смешанных чисел в неправильные дроби и обратно. Важно внимательно выполнять каждое действие, чтобы не потерять точность вычислений.