
Учебник по математике для 5 класса «Мнемозина» авторов Виленкин и Жохов представляет собой качественное пособие, которое активно используется в школьной программе. Этот учебник сочетает в себе подробные теоретические материалы, интересные задачи и увлекательные примеры, что делает его полезным инструментом для формирования базовых знаний и навыков у школьников.
ГДЗ по Математике 5 Класс Часть 2 Номер 4 Мнемозина Виленкин, Жохов — Подробные Ответы
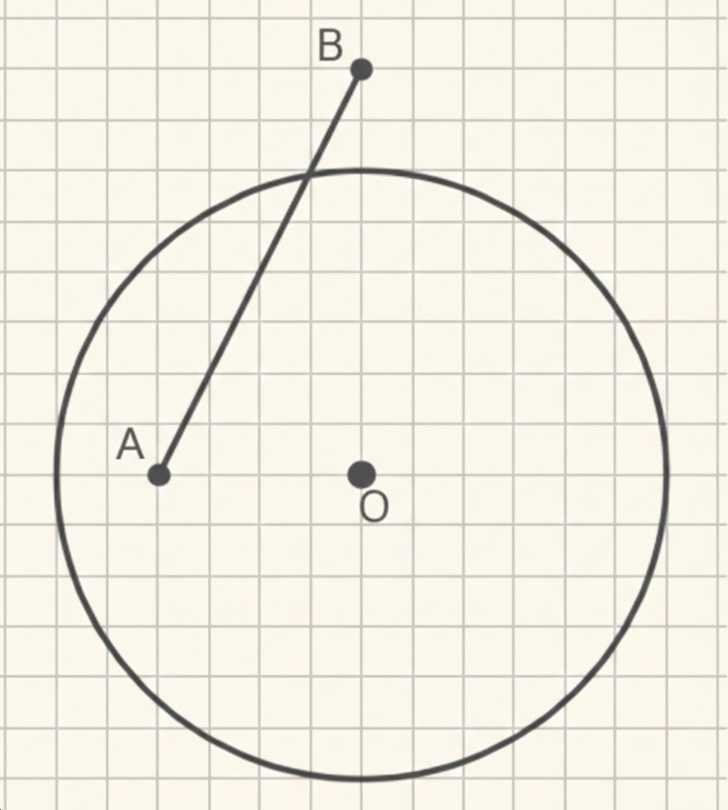
Изобразите круг, радиус которого 3 см. Отметьте точку \(A\) внутри круга и точку \(B\) вне круга. Измерьте расстояние от центра круга до точки \(A\) и до точки \(B\). Сравните эти расстояния с радиусом круга. Соедините точки \(A\) и \(B\) отрезком. Пересекается ли он с окружностью?
Расстояние от точки \(O\) до точки \(A\) равно 2 см, то есть \(OA = 2\) см.
Расстояние от точки \(O\) до точки \(B\) равно 4 см, то есть \(OB = 4\) см.
Радиус круга \(r = 3\) см.
Поскольку \(OA < r\), точка \(A\) лежит внутри круга. Поскольку \(OB > r\), точка \(B\) лежит вне круга.
Отрезок \(AB\), соединяющий точку внутри круга и точку вне круга, обязательно пересекает окружность.
Ответ: отрезок \(AB\) пересекается с окружностью.
Расстояние от точки \(O\) до точки \(A\) равно 2 см, что записывается как \(OA = 2\) см. Это означает, что точка \(A\) находится внутри круга, так как радиус круга равен \(r = 3\) см, а расстояние от центра до точки \(A\) меньше радиуса. Геометрически это значит, что точка \(A\) лежит внутри или на границе круга, но так как \(OA < r\), она именно внутри. Внутри круга все точки находятся на расстоянии, меньшем радиуса, от центра. Расстояние от точки \(O\) до точки \(B\) равно 4 см, то есть \(OB = 4\) см. Поскольку это расстояние больше радиуса круга \(r = 3\) см, точка \(B\) расположена вне круга. Вне круга находятся все точки, расстояние которых от центра превышает радиус. Таким образом, точка \(B\) лежит вне окружности, которая ограничивает круг. Отрезок \(AB\) соединяет точку \(A\), лежащую внутри круга, и точку \(B\), лежащую вне круга. По свойствам геометрии, если одна точка отрезка находится внутри круга, а другая — вне, то этот отрезок обязательно пересекает границу круга, то есть окружность. Следовательно, отрезок \(AB\) пересекает окружность ровно в одной точке. Это происходит потому, что при движении по отрезку из точки \(A\) (внутри) к точке \(B\) (снаружи) мы покидаем круг, и точка пересечения с окружностью — это граница круга, через которую отрезок выходит наружу.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!