ГДЗ по Математике 5 Класс Часть 2 Номер 37 Мнемозина Виленкин, Жохов — Подробные Ответы

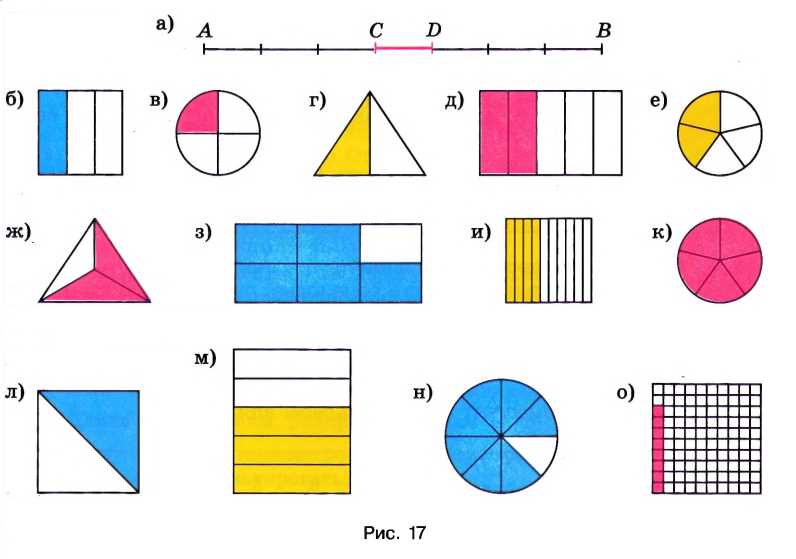
Какая часть фигуры закрашена (рис. 17)?

а) \( \frac{1}{7} \) часть отрезка \( AB \);

б) \( \frac{1}{3} \) часть квадрата;

в) \( \frac{1}{4} \) часть круга;

г) \( \frac{1}{2} \) часть треугольника;

д) \( \frac{2}{5} \) часть прямоугольника;

е) \( \frac{2}{5} \) часть круга;

ж) \( \frac{2}{3} \) часть треугольника;

з) \( \frac{5}{6} \) часть прямоугольника;

и) \( \frac{4}{10} \) часть квадрата;

к) \( \frac{5}{5} \) часть круга;

л) \( \frac{1}{2} \) часть квадрата;

м) \( \frac{3}{5} \) часть прямоугольника;

н) \( \frac{7}{8} \) часть круга;

о) \( \frac{8}{100} \) часть квадрата.

а) Закрашена \( \frac{1}{7} \) часть отрезка \( AB \). Это означает, что весь отрезок \( AB \) разделён на 7 равных частей, и закрашена ровно одна из них. Такой подход позволяет определить долю части от целого, где целое — длина отрезка \( AB \). Чтобы найти длину закрашенной части, нужно длину всего отрезка умножить на \( \frac{1}{7} \).

Деление отрезка на равные части и выделение одной из них — классический способ показать дробь как часть целого. Здесь дробь \( \frac{1}{7} \) показывает, что закрашенная часть составляет одну седьмую длины всего отрезка, что можно применить для измерения или сравнения частей отрезка.

б) Закрашена \( \frac{1}{3} \) часть квадрата. Это значит, что площадь квадрата условно разделена на три равные части, и одна из них закрашена. Поскольку площадь квадрата равна \( a^2 \), где \( a \) — длина стороны, закрашенная площадь будет равна \( a^2 \cdot \frac{1}{3} \).

Такое деление площади квадрата на равные части помогает понять, как дробь отражает часть площади фигуры. В данном случае \( \frac{1}{3} \) — это треть всей площади, и это можно использовать для решения задач на нахождение доли площади.

в) Закрашена \( \frac{1}{4} \) часть круга. Круг имеет площадь \( \pi r^2 \), где \( r \) — радиус. Деление круга на четыре равные части и выделение одной части соответствует выделению четверти площади круга, то есть \( \pi r^2 \cdot \frac{1}{4} \).

Такое деление часто используется для наглядного понимания дробей и частей круга, например, в задачах на вычисление площадей секторов. Дробь \( \frac{1}{4} \) показывает, что закрашенная часть — это четверть всего круга.

г) Закрашена \( \frac{1}{2} \) часть треугольника. Площадь треугольника равна \( \frac{1}{2}bh \), где \( b \) — основание, \( h \) — высота. Если треугольник разделён на две равные части, то каждая часть равна половине площади. Закрашенная часть — половина всего треугольника, то есть \( \frac{1}{2} \) от площади.

Такое деление часто используется для простого представления половины фигуры. Дробь \( \frac{1}{2} \) показывает, что закрашена ровно половина площади треугольника.

д) Закрашена \( \frac{2}{5} \) часть прямоугольника. Площадь прямоугольника равна \( ab \), где \( a \) и \( b \) — длины сторон. Деление на пять равных частей и выделение двух означает, что закрашено \( \frac{2}{5} \) от площади, то есть \( ab \cdot \frac{2}{5} \).

Этот пример показывает, как дробь с числителем больше единицы отражает несколько частей из нескольких равных. Закрашенная часть составляет две пятых всего прямоугольника, что можно использовать для вычислений долей.

е) Закрашена \( \frac{2}{5} \) часть круга. Аналогично предыдущему, площадь круга — \( \pi r^2 \). Деление круга на пять равных частей и выделение двух частей даёт закрашенную площадь \( \pi r^2 \cdot \frac{2}{5} \).

Дробь \( \frac{2}{5} \) показывает, что закрашено две части из пяти равных, что важно для понимания дробей с числителем, превышающим единицу.

ж) Закрашена \( \frac{2}{3} \) часть треугольника. Треугольник разделён на три равные части, и выделены две. Площадь закрашенной части равна \( \frac{2}{3} \) от всей площади, то есть \( \frac{2}{3} \cdot \frac{1}{2}bh \).

Такое деление помогает понять, как дробь выражает часть целого, когда числитель больше единицы, и как это применяется к фигурам.

з) Закрашена \( \frac{5}{6} \) часть прямоугольника. Здесь прямоугольник разделён на шесть равных частей, из которых выделены пять. Площадь закрашенной части равна \( ab \cdot \frac{5}{6} \).

Это пример дроби, близкой к целому (пять шестых), что показывает, как большая часть фигуры может быть выделена с помощью дробей.

и) Закрашена \( \frac{4}{10} \) часть квадрата. Площадь квадрата равна \( a^2 \), делённая на десять равных частей, из которых выделены четыре. Закрашенная площадь — \( a^2 \cdot \frac{4}{10} \).

Дробь \( \frac{4}{10} \) можно упростить до \( \frac{2}{5} \), что показывает взаимосвязь дробей и упрощение.

к) Закрашена вся часть круга, то есть \( \frac{5}{5} \) — это целый круг с площадью \( \pi r^2 \).

л) Закрашена \( \frac{1}{2} \) часть квадрата, то есть половина площади \( a^2 \cdot \frac{1}{2} \).

м) Закрашена \( \frac{3}{5} \) часть прямоугольника, площадь которого равна \( ab \cdot \frac{3}{5} \).

н) Закрашена \( \frac{7}{8} \) часть круга, площадь равна \( \pi r^2 \cdot \frac{7}{8} \).

о) Закрашена \( \frac{8}{100} \) часть квадрата, что равно \( a^2 \cdot \frac{8}{100} \), или \( a^2 \cdot 0{,}08 \).