ГДЗ по Математике 5 Класс Часть 2 Номер 36 Мнемозина Виленкин, Жохов — Подробные Ответы

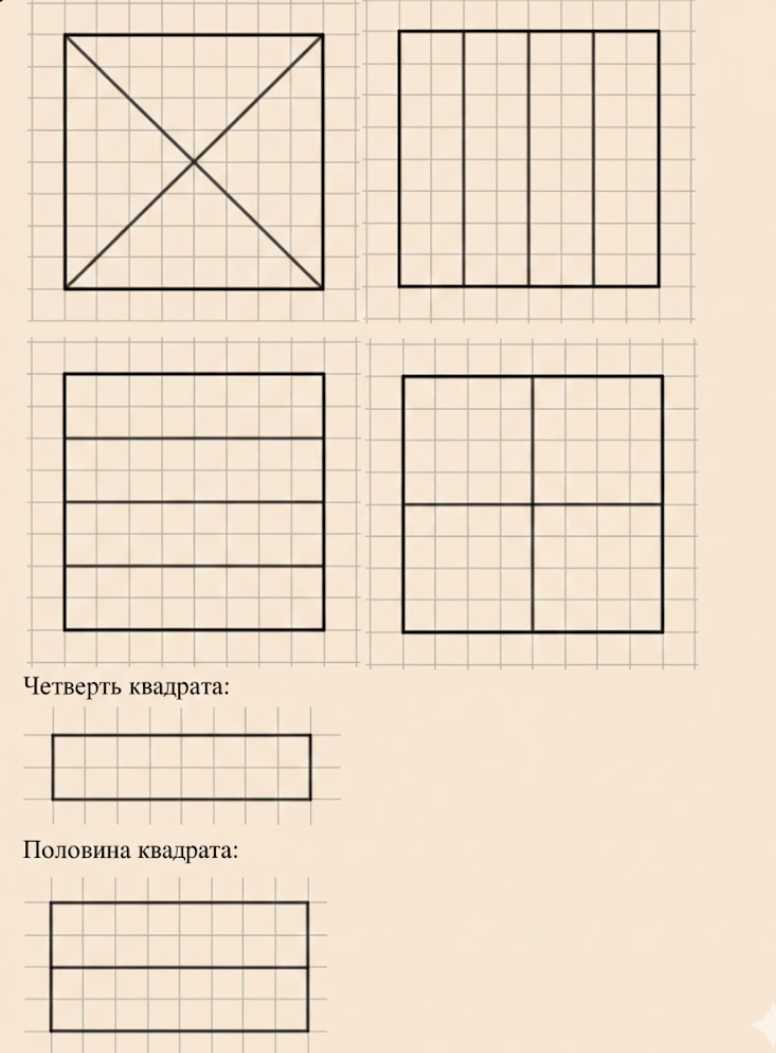
Разделите тремя способами квадрат со стороной 4 см на 4 доли. Начертите четверть квадрата, половину квадрата.

а) Разделить квадрат со стороной 4 см на 4 доли можно тремя способами:

1) Провести две диагонали квадрата, получив 4 треугольника равной площади.
2) Провести три вертикальные линии, разделив квадрат на 4 равные вертикальные полосы.
3) Провести три горизонтальные линии, разделив квадрат на 4 равные горизонтальные полосы.

б) Четверть квадрата — это часть квадрата, равная \( \frac{1}{4} \) от всей площади. Если сторона квадрата 4 см, то площадь квадрата \( 4 \times 4 = 16 \) см². Четверть квадрата — это площадь \( 16 \times \frac{1}{4} = 4 \) см². На рисунке четверть квадрата выделена как прямоугольник со сторонами 2 см и 4 см.

в) Половина квадрата — это часть квадрата, равная \( \frac{1}{2} \) от всей площади. Площадь половины квадрата равна \( 16 \times \frac{1}{2} = 8 \) см². На рисунке половина квадрата выделена как прямоугольник со сторонами 4 см и 2 см.

а) Чтобы разделить квадрат со стороной 4 см на 4 равные части, можно использовать несколько способов. Первый способ — провести две диагонали квадрата. Диагонали пересекаются в центре и делят квадрат на четыре треугольника с равными площадями. Это работает потому, что диагонали делят квадрат на четыре равных треугольника, у каждого из которых общая вершина в центре квадрата, а основания лежат на сторонах квадрата. Площадь каждого треугольника равна четверти площади квадрата.

Второй способ — провести три вертикальные линии, которые делят квадрат на четыре равные вертикальные полосы. Каждая полоса будет иметь ширину 1 см (поскольку сторона квадрата 4 см, то 4 разделить на 4 равно 1 см). Таким образом, площадь каждой полосы равна произведению ширины на высоту, то есть \(1 \times 4 = 4\) см², что составляет четверть площади всего квадрата. Третий способ — провести три горизонтальные линии, которые делят квадрат на четыре равные горизонтальные полосы. Аналогично вертикальному способу, каждая полоса будет иметь высоту 1 см и длину 4 см, то есть площадь тоже будет равна 4 см².

б) Четверть квадрата — это часть площади квадрата, равная \( \frac{1}{4} \) от всей площади. Площадь квадрата со стороной 4 см вычисляется по формуле площади квадрата \(S = a^2\), где \(a = 4\) см, следовательно, площадь квадрата равна \(4^2 = 16\) см². Чтобы найти четверть площади, нужно площадь квадрата умножить на \( \frac{1}{4} \), то есть \(16 \times \frac{1}{4} = 4\) см². На рисунке четверть квадрата изображена в виде прямоугольника со сторонами 2 см и 4 см. Это соответствует половине стороны квадрата по ширине и всей стороне по высоте, то есть площадь прямоугольника равна \(2 \times 4 = 8\) см², но так как это половина квадрата, а не четверть, то для четверти нужно взять половину от этого прямоугольника, например, прямоугольник 2 см на 2 см.

в) Половина квадрата — это часть площади, равная \( \frac{1}{2} \) от площади всего квадрата. Сначала вычисляем площадь квадрата: \(16\) см², как было указано ранее. Чтобы найти половину, площадь умножаем на \( \frac{1}{2} \), получаем \(16 \times \frac{1}{2} = 8\) см². На рисунке половина квадрата показана как прямоугольник со сторонами 4 см и 2 см, то есть высота равна половине стороны квадрата, а длина — всей стороне. Площадь такого прямоугольника равна \(4 \times 2 = 8\) см², что и составляет половину площади квадрата.

Таким образом, разделение квадрата на части и вычисление их площадей основано на простых геометрических свойствах и формуле площади квадрата. Важно понимать, что при делении квадрата на равные части площадь каждой части равна произведению соответствующих сторон, и сумма площадей всех частей равна площади всего квадрата.