ГДЗ по Математике 5 Класс Часть 2 Номер 35 Мнемозина Виленкин, Жохов — Подробные Ответы

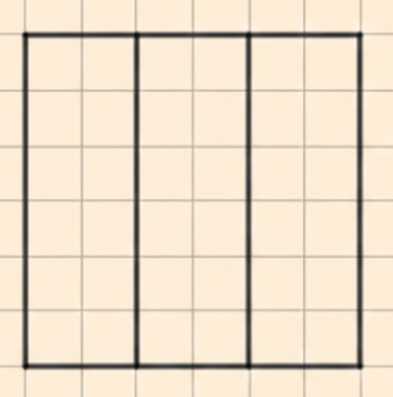
Начертите в тетради квадрат со стороной в 6 клеток. Разделите его на три доли. Начертите отдельно треть квадрата.

Квадрат со стороной 6 клеток имеет площадь \(6 \times 6 = 36\) клеток.

Разделим квадрат на три равные части вертикальными линиями, каждая часть будет иметь площадь \(\frac{36}{3} = 12\) клеток.

Треть квадрата — это прямоугольник размером 2 клетки в ширину и 6 клеток в высоту, площадь которого \(2 \times 6 = 12\) клеток.

а) Рассмотрим квадрат, у которого каждая сторона состоит из 6 клеток. Площадь такого квадрата определяется по формуле площади квадрата: умножаем длину стороны на саму себя. В данном случае это будет \(6 \times 6\). Поскольку каждая клетка считается единицей площади, то общее количество клеток, занимаемых квадратом, равно \(36\). Это означает, что весь квадрат покрывает ровно 36 маленьких квадратных клеток одинакового размера.

Для наглядности представим, что квадрат разбит на сетку из 6 строк и 6 столбцов клеток. Каждая клетка — это минимальный элемент площади, и их общее число равно произведению количества строк на количество столбцов, то есть \(6 \times 6 = 36\). Таким образом, площадь квадрата равна сумме площадей всех этих клеток.

б) Теперь разделим исходный квадрат на три равные вертикальные части. Для этого мы проведём две вертикальные линии, которые разделят квадрат на три прямоугольника одинаковой площади. Поскольку площадь всего квадрата равна \(36\), то площадь каждой из трёх частей будет равна \( \frac{36}{3} \). Вычисляя это, получаем, что площадь каждой части равна \(12\).

Каждая из этих частей — это прямоугольник, который занимает ровно треть площади исходного квадрата. Поскольку высота квадрата не меняется и равна 6 клеткам, то ширина каждого из этих прямоугольников должна быть такой, чтобы произведение ширины на высоту давало площадь 12. Это означает, что ширина прямоугольника равна \( \frac{12}{6} = 2 \) клетки.

в) Таким образом, каждая треть квадрата представляет собой прямоугольник размером 2 клетки в ширину и 6 клеток в высоту. Площадь такого прямоугольника вычисляется по формуле площади прямоугольника: умножаем ширину на высоту, то есть \(2 \times 6\). Результат равен 12 клеткам, что совпадает с вычисленной площадью одной трети квадрата.

Это подтверждает, что деление квадрата на три равные части вертикальными линиями приводит к образованию трёх прямоугольников одинаковой площади, каждый из которых занимает ровно одну треть площади исходного квадрата. Таким образом, можно визуально и математически убедиться, что площадь одной трети квадрата равна 12 клеткам.