ГДЗ по Математике 5 Класс Часть 2 Номер 337 Мнемозина Виленкин, Жохов — Подробные Ответы

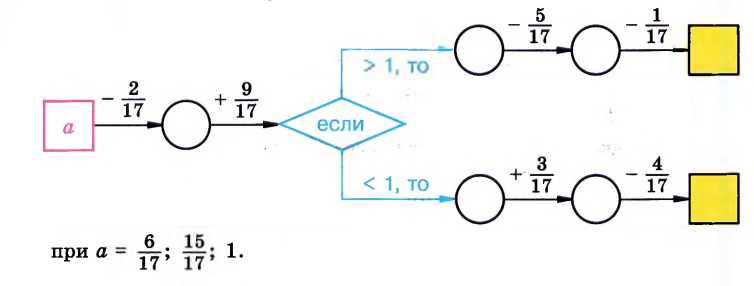
Восстановите цепочку вычислений

При \(a = \frac{6}{17}\):

\(\frac{6}{17} — \frac{2}{17} = \frac{4}{17}\);

\(\frac{4}{17} + \frac{9}{17} = \frac{13}{17} < 1\);

\(\frac{13}{17} + \frac{3}{17} = \frac{16}{17}\);

\(\frac{16}{17} — \frac{4}{17} = \frac{12}{17}\).

При \(a = \frac{15}{17}\):

\(\frac{15}{17} — \frac{2}{17} = \frac{13}{17}\);

\(\frac{13}{17} + \frac{9}{17} = \frac{22}{17} > 1\);

\(\frac{22}{17} — \frac{5}{17} = \frac{17}{17}\);

\(\frac{17}{17} — \frac{1}{17} = \frac{16}{17}\).

При \(a = 1\):

\(1 — \frac{2}{17} = \frac{15}{17}\);

\(\frac{15}{17} + \frac{9}{17} = \frac{24}{17} > 1\);

\(\frac{24}{17} — \frac{5}{17} = \frac{19}{17}\);

\(\frac{19}{17} — \frac{1}{17} = \frac{18}{17} = 1 \frac{1}{17}\).

а) При \(a = \frac{6}{17}\) сначала вычисляем разность \(\frac{6}{17} — \frac{2}{17}\). Поскольку знаменатели равны, вычитаем числители: \(6 — 2 = 4\), получая \(\frac{4}{17}\). Это значение показывает, насколько \(a\) уменьшилось на \(\frac{2}{17}\).

Далее складываем \(\frac{4}{17} + \frac{9}{17}\). Сложение дробей с одинаковыми знаменателями выполняется через сложение числителей: \(4 + 9 = 13\), получается \(\frac{13}{17}\). Это значение меньше 1, что важно для сравнения с единицей, так как показывает, что сумма не превышает целое число.

Затем прибавляем \(\frac{13}{17} + \frac{3}{17} = \frac{16}{17}\). Это значение ближе к 1, но всё ещё меньше. Наконец, вычитаем \(\frac{16}{17} — \frac{4}{17} = \frac{12}{17}\), что показывает уменьшение результата на \(\frac{4}{17}\) и завершает вычисления для этого случая.

б) При \(a = \frac{15}{17}\) начинаем с вычисления \(\frac{15}{17} — \frac{2}{17} = \frac{13}{17}\), что уменьшает исходное значение на \(\frac{2}{17}\). Это позволяет понять, как меняется величина \(a\) при вычитании.

Следующий шаг — сложение \(\frac{13}{17} + \frac{9}{17} = \frac{22}{17}\). Эта сумма больше 1, что указывает на превышение целого значения, то есть сумма дробей теперь больше единицы, что важно при анализе неравенств.

Далее вычитаем \(\frac{22}{17} — \frac{5}{17} = \frac{17}{17}\), что равно 1. Это показывает, что после вычитания результат становится ровно целым числом. Затем вычисляем \(\frac{17}{17} — \frac{1}{17} = \frac{16}{17}\), что немного уменьшает значение, но остаётся меньше единицы.

в) При \(a = 1\) сначала вычисляем \(1 — \frac{2}{17}\). Представляя 1 как \(\frac{17}{17}\), вычитаем \(\frac{2}{17}\), получая \(\frac{15}{17}\). Это уменьшение показывает, как от единицы отнимается дробное число.

Затем складываем \(\frac{15}{17} + \frac{9}{17} = \frac{24}{17}\). Сумма больше единицы, что означает превышение целого числа, важное для анализа значений.

Далее вычитаем \(\frac{24}{17} — \frac{5}{17} = \frac{19}{17}\), что всё ещё больше 1. После этого вычисляем \(\frac{19}{17} — \frac{1}{17} = \frac{18}{17}\), что можно записать как \(1 \frac{1}{17}\), показывая смешанное число, превышающее единицу.