ГДЗ по Математике 5 Класс Часть 2 Номер 3 Мнемозина Виленкин, Жохов — Подробные Ответы

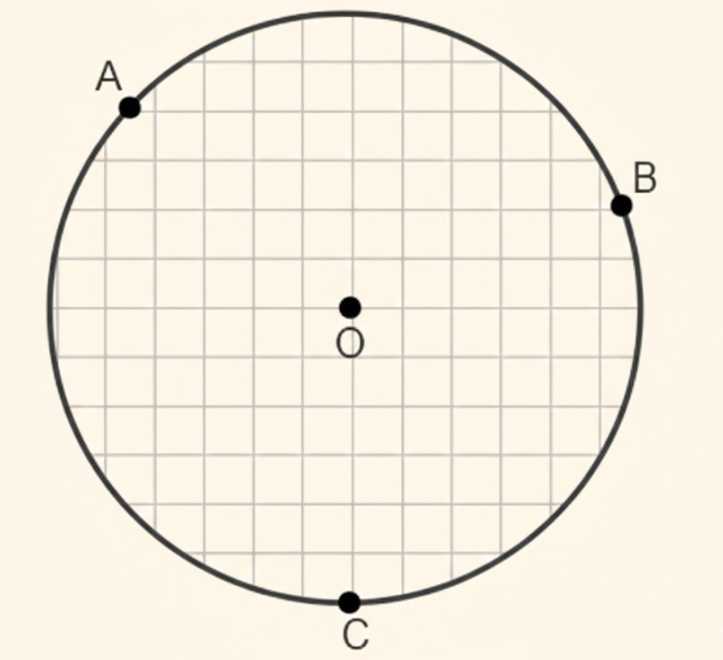
Начертите окружность и отметьте на ней три точки \(A\), \(B\) и \(C\). Назовите дуги, на которые эти точки делят окружность.

Дуги: \(AB\), \(BC\), \(AC\).

Дуги \(AB\), \(BC\), \(AC\) — это части окружности, ограниченные точками \(A\), \(B\) и \(C\), которые лежат на этой окружности. Каждая дуга представляет собой непрерывный участок окружности между двумя заданными точками. Точки \(A\), \(B\) и \(C\) являются концами этих дуг, а центр окружности \(O\) служит для определения радиуса и углов, связанных с этими дугами. Понимание дуг важно для изучения свойств окружности и углов, которые они образуют.

Дуга \(AB\) — это часть окружности, соединяющая точки \(A\) и \(B\). Аналогично, дуга \(BC\) соединяет точки \(B\) и \(C\), а дуга \(AC\) — точки \(A\) и \(C\). Эти дуги можно рассматривать как сегменты окружности, длина которых зависит от угла, заключенного между радиусами \(OA\), \(OB\) и \(OC\). Дуги могут быть как меньшими, так и большими, но в данном случае подразумеваются именно меньшие дуги, так как они ограничены ближайшими точками на окружности.

Центр окружности \(O\) играет ключевую роль, так как расстояние от \(O\) до любой точки на окружности (включая \(A\), \(B\), \(C\)) одинаково и равно радиусу \(r\). Радиусы \(OA\), \(OB\), \(OC\) образуют углы, по которым можно вычислить длины дуг с помощью формулы длины дуги \(l = r \alpha\), где \(\alpha\) — центральный угол в радианах, соответствующий дуге. Таким образом, дуги \(AB\), \(BC\), \(AC\) — это основные элементы окружности, определяемые точками на ней и центром \(O\).