ГДЗ по Математике 5 Класс Часть 2 Номер 278 Мнемозина Виленкин, Жохов — Подробные Ответы

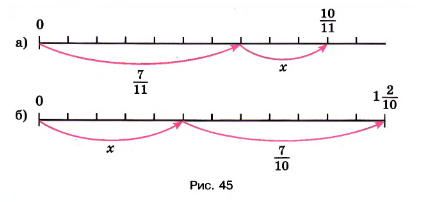
По рисунку 45 составьте уравнение и решите его.

а) \( \frac{7}{11} + x = \frac{10}{11} \)

\( x = \frac{10}{11} — \frac{7}{11} \)

\( x = \frac{3}{11} \)

Ответ: \( \frac{3}{11} \).

б) \( x + \frac{7}{10} = 1 \frac{2}{10} \)

\( x = 1 \frac{2}{10} — \frac{7}{10} \)

\( x = \frac{12}{10} — \frac{7}{10} \)

\( x = \frac{5}{10} \)

Ответ: \( \frac{5}{10} \).

а) Рассмотрим уравнение \( \frac{7}{11} + x = \frac{10}{11} \). Здесь нам нужно найти неизвестное \(x\), которое при сложении с дробью \( \frac{7}{11} \) даст в результате \( \frac{10}{11} \). Чтобы найти \(x\), нужно из правой части уравнения вычесть левую часть без \(x\), то есть вычесть \( \frac{7}{11} \) из \( \frac{10}{11} \). Поскольку знаменатели у дробей одинаковые (оба равны 11), вычитание выполняется просто — вычитаем числители, а знаменатель оставляем тот же.

Выполняем вычитание: \( x = \frac{10}{11} — \frac{7}{11} = \frac{10 — 7}{11} = \frac{3}{11} \). Таким образом, значение \(x\) равно \( \frac{3}{11} \). Это означает, что если к \( \frac{7}{11} \) прибавить \( \frac{3}{11} \), то сумма будет равна \( \frac{10}{11} \), что соответствует условию уравнения.

б) Уравнение \( x + \frac{7}{10} = 1 \frac{2}{10} \) содержит смешанное число \(1 \frac{2}{10}\), которое удобнее преобразовать в неправильную дробь для упрощения вычислений. Для этого умножаем целую часть 1 на знаменатель 10 и прибавляем числитель 2: \(1 \times 10 + 2 = 12\), значит \(1 \frac{2}{10} = \frac{12}{10}\). Теперь уравнение выглядит как \( x + \frac{7}{10} = \frac{12}{10} \).

Чтобы найти \(x\), нужно из правой части уравнения вычесть левую часть без \(x\), то есть вычесть \( \frac{7}{10} \) из \( \frac{12}{10} \). Поскольку знаменатели одинаковы, вычитаем числители: \( x = \frac{12}{10} — \frac{7}{10} = \frac{12 — 7}{10} = \frac{5}{10} \). Значит, \(x = \frac{5}{10}\). Это значение удовлетворяет исходному уравнению: если к \( \frac{5}{10} \) прибавить \( \frac{7}{10} \), получится \( \frac{12}{10} \), что равно \(1 \frac{2}{10}\).