ГДЗ по Математике 5 Класс Часть 2 Номер 272 Мнемозина Виленкин, Жохов — Подробные Ответы

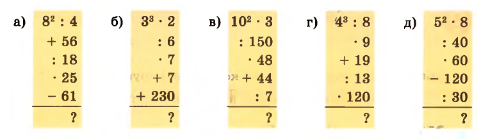
Вычислите устно:

а) \(8^2 : 4 = 64 : 4 = 16;\)
\(16 + 56 = 72;\)
\(72 : 18 = 4;\)
\(4 \cdot 25 = 100;\)
\(100 — 61 = 39.\)

б) \(3^3 \cdot 2 = 27 \cdot 2 = 54;\)
\(54 : 6 = 9;\)
\(9 \cdot 7 = 63;\)
\(63 + 7 = 70;\)
\(70 + 230 = 300.\)

в) \(10^2 \cdot 3 = 100 \cdot 3 = 300;\)
\(300 : 150 = 2;\)
\(2 \cdot 48 = 96;\)
\(96 + 44 = 140;\)
\(140 : 7 = 20.\)

г) \(4^3 : 8 = 64 : 8 = 8;\)
\(8 \cdot 9 = 72;\)
\(72 + 19 = 91;\)
\(91 : 13 = 7;\)
\(7 \cdot 120 = 840.\)

д) \(5^2 \cdot 8 = 25 \cdot 8 = 200;\)
\(200 : 40 = 5;\)
\(5 \cdot 60 = 300;\)
\(300 — 120 = 180;\)
\(180 : 30 = 6.\)

а) Сначала вычисляем степень числа 8 в квадрате, то есть \(8^2 = 64\). Далее делим это число на 4: \(64 : 4 = 16\). Это действие показывает, что мы последовательно уменьшаем число, деля его на одинаковое число — 4. Затем к полученному результату прибавляем 56: \(16 + 56 = 72\). Здесь мы переходим от деления к сложению, чтобы увеличить значение. Следующий шаг — деление числа 72 на 18: \(72 : 18 = 4\). Это уменьшает число снова, и результат становится 4. После этого умножаем 4 на 25: \(4 \cdot 25 = 100\), что значительно увеличивает значение. В конце вычитаем из 100 число 61: \(100 — 61 = 39\), что уменьшает итоговый результат. Таким образом, последовательность операций чередует деление, сложение, умножение и вычитание, что приводит к окончательному значению 39.

б) Начинаем с возведения числа 3 в куб: \(3^3 = 27\). Умножаем это на 2: \(27 \cdot 2 = 54\), что удваивает исходное значение. Затем делим 54 на 6: \(54 : 6 = 9\), уменьшая число в шесть раз. Следующий шаг — умножение на 7: \(9 \cdot 7 = 63\), что снова увеличивает результат. Прибавляем к 63 число 7: \(63 + 7 = 70\), увеличивая сумму. Последним действием является прибавление 230 к 70: \(70 + 230 = 300\). В этом примере мы видим чередование операций умножения, деления и сложения, которые постепенно изменяют число от небольшого к более крупному.

в) Сначала возводим 10 в квадрат: \(10^2 = 100\). Умножаем на 3: \(100 \cdot 3 = 300\), увеличивая число в три раза. Делим 300 на 150: \(300 : 150 = 2\), что значительно уменьшает результат. Умножаем 2 на 48: \(2 \cdot 48 = 96\), увеличивая значение почти в 50 раз. Прибавляем 44 к 96: \(96 + 44 = 140\), что увеличивает сумму. В конце делим 140 на 7: \(140 : 7 = 20\), уменьшая число. В этом примере операции деления и умножения чередуются с сложением, что позволяет постепенно изменять исходное число.

г) Возводим 4 в куб: \(4^3 = 64\). Делим 64 на 8: \(64 : 8 = 8\), уменьшая число в 8 раз. Далее умножаем 8 на 9: \(8 \cdot 9 = 72\), увеличивая результат. Прибавляем 19 к 72: \(72 + 19 = 91\), увеличивая сумму. Затем делим 91 на 13: \(91 : 13 = 7\), что уменьшает число. Последний этап — умножение 7 на 120: \(7 \cdot 120 = 840\), что значительно увеличивает итоговое значение. Здесь операции деления и умножения сопровождаются сложением, что позволяет гибко изменять число.

д) Возводим 5 в квадрат: \(5^2 = 25\). Умножаем 25 на 8: \(25 \cdot 8 = 200\), увеличивая значение. Делим 200 на 40: \(200 : 40 = 5\), уменьшая число. Умножаем 5 на 60: \(5 \cdot 60 = 300\), увеличивая результат. Вычитаем 120 из 300: \(300 — 120 = 180\), уменьшая сумму. В конце делим 180 на 30: \(180 : 30 = 6\), что уменьшает число. В этом примере чередуются операции умножения, деления и вычитания, что позволяет получить итоговое значение 6.