ГДЗ по Математике 5 Класс Часть 2 Номер 27 Мнемозина Виленкин, Жохов — Подробные Ответы

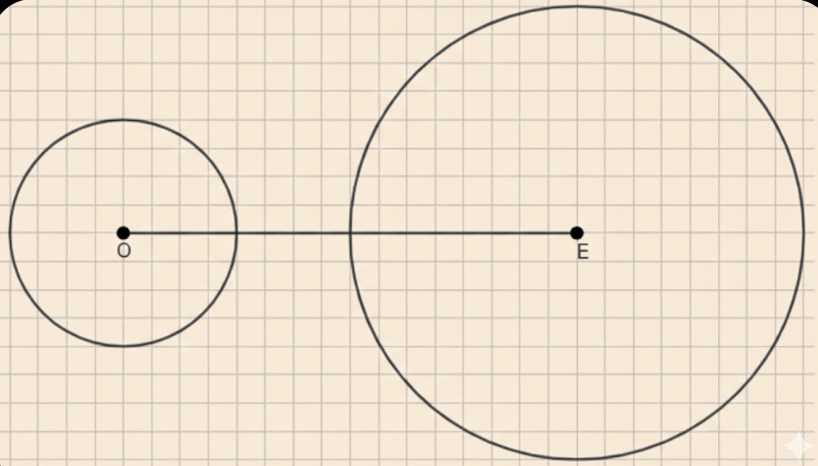
Отметьте точки \(O\) и \(E\) так, чтобы \(OE = 8\) см. Постройте окружность с центром \(O\) и радиусом 2 см и окружность с центром \(E\) и радиусом 4 см. Пересекаются ли эти окружности?

Две окружности имеют центры в точках \( O \) и \( E \) и радиусы, равные расстояниям от этих центров до точек на окружностях. Расстояние между центрами обозначено отрезком \( OE \). На рисунке видно, что расстояние \( OE \) больше суммы радиусов обеих окружностей.

Поскольку расстояние между центрами \( OE \) больше суммы радиусов, окружности не пересекаются. Это значит, что ни одна точка первой окружности не совпадает с точкой второй, и множество точек пересечения равно \(\emptyset\).

Таким образом, условие непересечения окружностей формально выражается неравенством \( OE > r_1 + r_2 \), где \( r_1 \) и \( r_2 \) — радиусы окружностей с центрами в \( O \) и \( E \) соответственно.

Две окружности на рисунке имеют центры в точках \( O \) и \( E \), а также радиусы, которые равны расстояниям от этих центров до точек на соответствующих окружностях. Расстояние между центрами обозначено отрезком \( OE \). На изображении видно, что отрезок \( OE \) значительно длиннее, чем радиусы обеих окружностей, то есть расстояние между центрами больше суммы радиусов. Это ключевой фактор, определяющий взаимное расположение окружностей.

Если рассмотреть условие пересечения окружностей, оно требует, чтобы расстояние между центрами было не больше суммы радиусов, то есть выполнялось неравенство \( OE \leq r_1 + r_2 \), где \( r_1 \) и \( r_2 \) — радиусы окружностей с центрами в \( O \) и \( E \) соответственно. В нашем случае это условие нарушается, так как \( OE > r_1 + r_2 \). Следовательно, окружности не имеют общих точек, то есть они не пересекаются. Это означает, что множество точек пересечения равно \(\emptyset\).

Кроме того, геометрически это можно объяснить так: каждая окружность задаётся множеством точек, находящихся на фиксированном расстоянии от своего центра. Если расстояние между центрами слишком велико, то ни одна точка первой окружности не может совпасть с точкой второй, так как для этого необходимо, чтобы расстояния от центров до общей точки были равны радиусам. Поскольку расстояние между центрами больше суммы радиусов, эти множества не пересекаются, и окружности не имеют общих точек.