ГДЗ по Математике 5 Класс Часть 2 Номер 26 Мнемозина Виленкин, Жохов — Подробные Ответы

Отметьте две точки \(K\) и \(P\) так, чтобы \(KP = 6\) см. Постройте окружность с центром \(K\) и радиусом 5 см и окружность с центром \(P\) и радиусом 4 см. Пересекаются ли эти окружности?

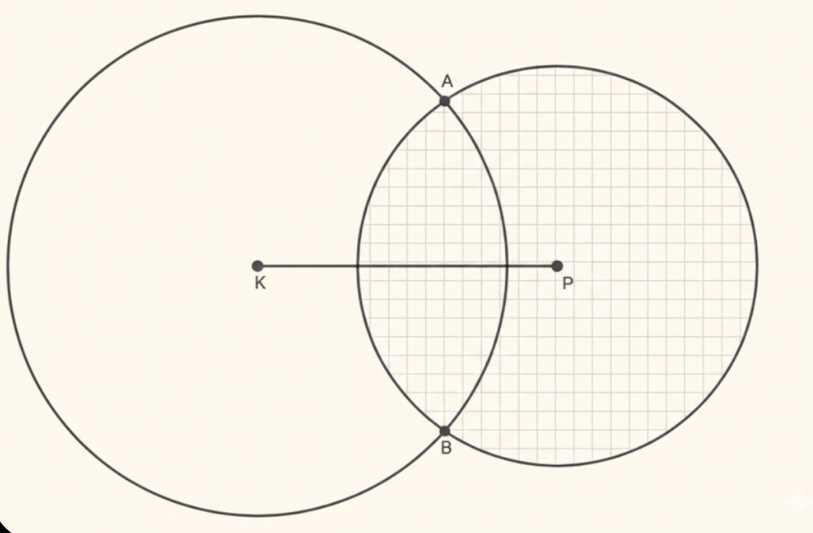
Даны две окружности, пересекающиеся в двух точках: \( A \) и \( B \).

Точки \( K \) и \( P \) — центры окружностей.

Отрезок \( KP \) — расстояние между центрами окружностей.

Точки \( A \) и \( B \) — точки пересечения окружностей, лежат на обеих окружностях.

Две окружности на рисунке имеют центры в точках \( K \) и \( P \). Расстояние между этими центрами обозначено отрезком \( KP \). Каждая окружность задана своим радиусом: радиус первой окружности равен расстоянию от \( K \) до любой точки на её окружности, а радиус второй — от \( P \) до любой точки на её окружности. Эти радиусы могут быть разными, что видно по разным размерам окружностей на рисунке.

Окружности пересекаются в двух точках \( A \) и \( B \). Эти точки принадлежат одновременно обеим окружностям, то есть расстояние от \( A \) до \( K \) равно радиусу первой окружности, а расстояние от \( A \) до \( P \) равно радиусу второй. Аналогично для точки \( B \). Пересечение двух окружностей в двух точках возможно тогда, когда расстояние между центрами \( KP \) меньше суммы радиусов, но больше разности радиусов, то есть выполняется неравенство \( |r_1 — r_2| < KP < r_1 + r_2 \). Точки \( A \) и \( B \) лежат на прямой, проходящей через эти точки пересечения, которая называется хордой пересечения. Эта хорда перпендикулярна отрезку \( KP \) и делит его на две части. Таким образом, геометрически можно определить положение точек пересечения, используя свойства радиусов, расстояния между центрами и прямоугольных треугольников, образуемых радиусами и хордой \( AB \). Это ключевой момент для вычисления координат точек пересечения или анализа взаимного расположения окружностей.