ГДЗ по Математике 5 Класс Часть 2 Номер 251 Мнемозина Виленкин, Жохов — Подробные Ответы

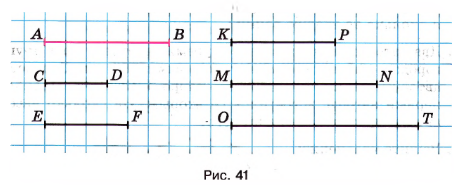
Какую часть длины отрезка \(AB\) составляет длина каждого отрезка на рисунке 41?

Отрезок \( CD \) составляет \( \frac{1}{2} \) часть отрезка \( AB \).

Отрезок \( EF \) составляет \( \frac{2}{3} \) часть отрезка \( AB \).

Отрезок \( KP \) составляет \( \frac{5}{6} \) часть отрезка \( AB \).

Отрезок \( MN \) составляет \( \frac{7}{6} \) часть отрезка \( AB \).

Отрезок \( OT \) составляет \( \frac{9}{6} \) часть отрезка \( AB \).

Отрезок \( CD \) составляет \( \frac{1}{2} \) часть отрезка \( AB \). Это значит, что длина \( CD \) равна половине длины всего отрезка \( AB \). Если длина \( AB \) равна некоторому числу \( x \), то длина \( CD \) будет равна \( \frac{1}{2}x \). Таким образом, \( CD \) занимает ровно половину всего отрезка \( AB \), что можно представить как деление отрезка \( AB \) на две равные части.

Отрезок \( EF \) составляет \( \frac{2}{3} \) часть отрезка \( AB \). Это означает, что длина \( EF \) равна двум третям длины отрезка \( AB \). Если длина \( AB \) равна \( x \), то длина \( EF \) будет равна \( \frac{2}{3}x \). Дробь \( \frac{2}{3} \) показывает, что \( EF \) больше половины отрезка \( AB \), но меньше самого отрезка, и занимает примерно 66,7% длины \( AB \).

Отрезок \( KP \) составляет \( \frac{5}{6} \) часть отрезка \( AB \). Здесь длина \( KP \) почти равна длине всего отрезка \( AB \), так как \( \frac{5}{6} \) — это большая часть, близкая к единице. Если \( AB = x \), то \( KP = \frac{5}{6}x \). Это значит, что \( KP \) занимает около 83,3% длины \( AB \), что значительно больше половины и двух третей.

Отрезок \( MN \) составляет \( \frac{7}{6} \) часть отрезка \( AB \). Дробь \( \frac{7}{6} \) больше единицы, что означает, что длина \( MN \) превышает длину \( AB \). Если \( AB = x \), то \( MN = \frac{7}{6}x \), то есть \( MN \) длиннее \( AB \) примерно на одну шестую. Это может означать, что отрезок \( MN \) выходит за пределы \( AB \) или относится к другому контексту, где длина превышает исходный отрезок.

Отрезок \( OT \) составляет \( \frac{9}{6} \) часть отрезка \( AB \). Эта дробь также больше единицы, поскольку \( \frac{9}{6} = \frac{3}{2} \). Значит, длина \( OT \) равна полутора длинам отрезка \( AB \). Если \( AB = x \), то \( OT = \frac{3}{2}x \), что на 50% больше длины \( AB \). Это указывает на то, что \( OT \) значительно длиннее отрезка \( AB \), и его длина превышает длину исходного отрезка на половину.