ГДЗ по Математике 5 Класс Часть 2 Номер 250 Мнемозина Виленкин, Жохов — Подробные Ответы

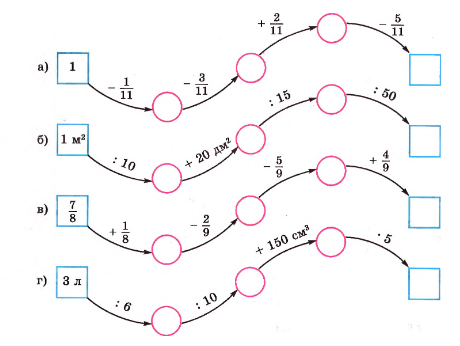
Восстановите цепочку вычислений:

a) \(1 — \frac{1}{11} = \frac{11}{11} — \frac{1}{11} = \frac{10}{11}\);
\(\frac{10}{11} — \frac{3}{11} = \frac{7}{11}\);
\(\frac{7}{11} + \frac{2}{11} = \frac{9}{11}\);
\(\frac{9}{11} — \frac{5}{11} = \frac{4}{11}\).

б) \(1 \text{ м}^2 = 100 \text{ дм}^2\);
\(100 \text{ дм}^2 : 10 = 10 \text{ дм}^2\);
\(10 \text{ дм}^2 + 20 \text{ дм}^2 = 30 \text{ дм}^2\);
\(30 \text{ дм}^2 : 15 = 2 \text{ дм}^2\);
\(2 \text{ дм}^2 = 200 \text{ см}^2\);
\(200 \text{ см}^2 : 50 = 4 \text{ см}^2\).

в) \(\frac{7}{8} + \frac{1}{8} = \frac{8}{8} = 1\);
\(1 — \frac{2}{9} = \frac{9}{9} — \frac{2}{9} = \frac{7}{9}\);
\(\frac{7}{9} — \frac{5}{9} = \frac{2}{9}\);
\(\frac{2}{9} + \frac{4}{9} = \frac{6}{9}\).

г) \(3 \text{ л} = 3000 \text{ см}^3\);
\(3000 \text{ см}^3 : 6 = 500 \text{ см}^3\);
\(500 \text{ см}^3 : 10 = 50 \text{ см}^3\);
\(50 \text{ см}^3 + 150 \text{ см}^3 = 200 \text{ см}^3\);
\(200 \text{ см}^3 \times 5 = 1000 \text{ см}^3\);
\(1000 \text{ см}^3 = 1 \text{ л}\).

а) Рассмотрим выражение \(1 — \frac{1}{11}\). Чтобы вычесть дробь из целого числа, нужно представить целое число в виде дроби с тем же знаменателем, то есть \(1 = \frac{11}{11}\). Тогда вычитание становится \(\frac{11}{11} — \frac{1}{11} = \frac{10}{11}\). Это значит, что если у нас есть целая часть, и мы вычитаем из неё одну одиннадцатую, то остаётся десять одиннадцатых.

Далее, из результата \(\frac{10}{11}\) вычитаем \(\frac{3}{11}\). Поскольку знаменатели одинаковые, просто вычитаем числители: \(10 — 3 = 7\), получаем \(\frac{7}{11}\). Следующий шаг — прибавить к \(\frac{7}{11}\) дробь \(\frac{2}{11}\). Сложение с одинаковыми знаменателями также сводится к сложению числителей: \(7 + 2 = 9\), итого \(\frac{9}{11}\). В конце вычитаем \(\frac{5}{11}\) из \(\frac{9}{11}\), получая \(\frac{9 — 5}{11} = \frac{4}{11}\). Таким образом, каждый шаг связан с операциями над дробями с одинаковым знаменателем, что упрощает вычисления.

б) В этом пункте мы работаем с единицами площади. Известно, что \(1 \text{ м}^2 = 100 \text{ дм}^2\), то есть один квадратный метр равен ста квадратным дециметрам. Следующее действие — деление \(100 \text{ дм}^2\) на 10, что даёт \(10 \text{ дм}^2\). Это показывает, как уменьшается площадь при делении. Затем прибавляем \(10 \text{ дм}^2\) и \(20 \text{ дм}^2\), получая \(30 \text{ дм}^2\), что соответствует сумме двух площадей.

После этого \(30 \text{ дм}^2\) делим на 15, получая \(2 \text{ дм}^2\). Это демонстрирует, как площадь уменьшается при делении на число. Переводим \(2 \text{ дм}^2\) в квадратные сантиметры, учитывая, что \(1 \text{ дм}^2 = 100 \text{ см}^2\), следовательно, \(2 \text{ дм}^2 = 200 \text{ см}^2\). Далее делим \(200 \text{ см}^2\) на 50, получая \(4 \text{ см}^2\). Этот процесс показывает связь между разными единицами площади и операции с ними.

в) Здесь рассматриваются дроби с разными знаменателями, но в примере знаменатели одинаковы, что упрощает вычисления. Сначала складываем \(\frac{7}{8}\) и \(\frac{1}{8}\). При одинаковом знаменателе складываем числители: \(7 + 1 = 8\), получаем \(\frac{8}{8} = 1\). Это показывает, что сумма дробей с одинаковым знаменателем, числители которых в сумме равны знаменателю, равна единице.

Далее вычитаем из 1 дробь \(\frac{2}{9}\). Представляем 1 как \(\frac{9}{9}\) и вычитаем: \(\frac{9}{9} — \frac{2}{9} = \frac{7}{9}\). Следующее действие — вычитание \(\frac{5}{9}\) из \(\frac{7}{9}\), что даёт \(\frac{2}{9}\). Наконец, прибавляем \(\frac{4}{9}\) к \(\frac{2}{9}\), получая \(\frac{6}{9}\). Все операции основаны на сложении и вычитании дробей с одинаковым знаменателем, что упрощает вычисления.

г) В этом пункте рассматриваются объёмы и их переводы между литрами и кубическими сантиметрами. Известно, что \(3 \text{ л} = 3000 \text{ см}^3\), так как 1 литр равен 1000 кубическим сантиметрам. Следующее действие — деление \(3000 \text{ см}^3\) на 6, что даёт \(500 \text{ см}^3\). Это показывает, как уменьшается объём при делении.

Далее делим \(500 \text{ см}^3\) на 10, получая \(50 \text{ см}^3\). После этого прибавляем \(50 \text{ см}^3\) и \(150 \text{ см}^3\), что даёт \(200 \text{ см}^3\). Следующий шаг — умножение \(200 \text{ см}^3\) на 5, что равно \(1000 \text{ см}^3\). Наконец, переводим \(1000 \text{ см}^3\) обратно в литры, получая \(1 \text{ л}\). Этот процесс демонстрирует взаимосвязь единиц объёма и операции с ними.