ГДЗ по Математике 5 Класс Часть 2 Номер 25 Мнемозина Виленкин, Жохов — Подробные Ответы

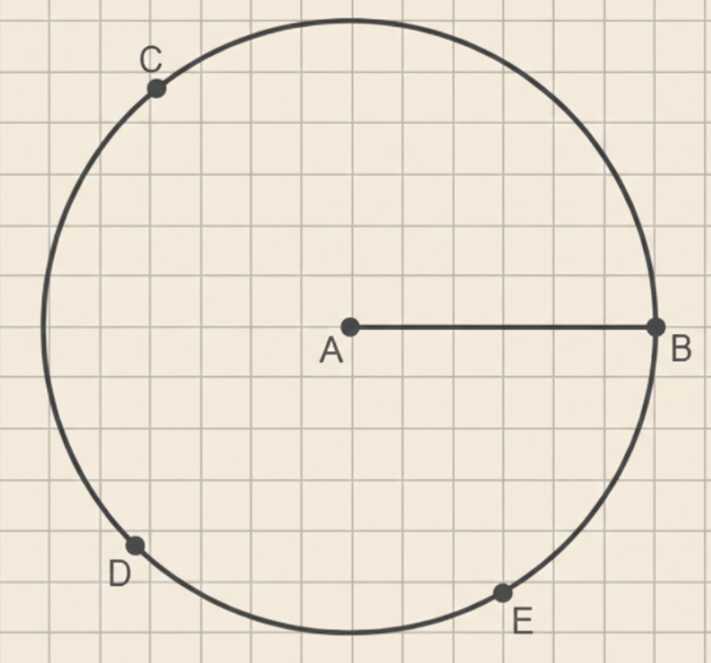
Отметьте две точки А и В так, чтобы \(AB = 3\) см. С помощью циркуля постройте ещё три точки \(C\), \(D\) и \(E\), которые находились бы от точки \(A\) на расстоянии 3 см.

Точки \(C\), \(D\) и \(E\) находятся на расстоянии 3 см от точки \(A\), значит радиус окружности равен \(3\) см.

Длина отрезка \(AB\) равна радиусу, то есть \(AB = 3\) см.

Ответ: \(3\) см.

Точки \(C\), \(D\) и \(E\) лежат на окружности, центр которой отмечен точкой \(A\). В условии сказано, что расстояние от точки \(A\) до каждой из этих точек равно 3 см. Это означает, что все три точки находятся на одинаковом расстоянии от центра \(A\), то есть они лежат на окружности с радиусом равным 3 см. Радиус окружности — это расстояние от центра до любой точки на окружности, поэтому \(AC = AD = AE = 3\) см.

На рисунке видно, что точка \(B\) лежит на той же линии, что и точка \(A\), и расположена на окружности. Поскольку \(B\) находится на границе окружности, расстояние от \(A\) до \(B\) также равно радиусу окружности. Следовательно, длина отрезка \(AB\) равна 3 см. Это ключевой момент, так как по условию все точки, которые лежат на окружности, удалены от центра на одинаковое расстояние.

Таким образом, исходя из определения окружности и данных условий, радиус окружности равен 3 см, и отрезок \(AB\), соединяющий центр с точкой на окружности, тоже равен 3 см. Значит, \(AB = 3\) см. Это значение является длиной радиуса окружности, на которой лежат точки \(C\), \(D\) и \(E\).