ГДЗ по Математике 5 Класс Часть 2 Номер 239 Мнемозина Виленкин, Жохов — Подробные Ответы

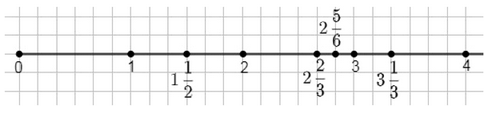
Примите за единичный отрезок длину 6 клеток тетради и отметьте на координатном луче точки с координатами:

\(3 \frac{1}{3}\); \(2 \frac{5}{6}\); \(2 \frac{2}{3}\); \(1 \frac{1}{2}\).

а) \(1 \frac{1}{2} = \frac{3}{2}\)

б) \(2 \frac{2}{3} = \frac{8}{3}\)

в) \(3 \frac{1}{3} = \frac{10}{3}\)

г) \(2 \frac{5}{6} = \frac{17}{6}\)

а) Для перевода смешанного числа \(1 \frac{1}{2}\) в неправильную дробь нужно умножить целую часть на знаменатель дробной части и прибавить числитель. Здесь целая часть равна 1, знаменатель дроби 2, числитель 1. Выполняем вычисление: \(1 \times 2 + 1 = 3\). Полученное число становится числителем новой дроби, а знаменатель остается прежним — 2. Таким образом, смешанное число \(1 \frac{1}{2}\) преобразуется в дробь \(\frac{3}{2}\).

Такое преобразование удобно для дальнейших арифметических операций с дробями, так как неправильные дроби легче складывать, вычитать, умножать и делить. В данном случае \(\frac{3}{2}\) показывает, что значение больше единицы, что соответствует исходному смешанному числу.

б) В смешанном числе \(2 \frac{2}{3}\) целая часть равна 2, а дробная часть — \(\frac{2}{3}\). Чтобы перевести это в неправильную дробь, умножаем целую часть на знаменатель дроби: \(2 \times 3 = 6\), затем прибавляем числитель: \(6 + 2 = 8\). Получаем числитель 8, а знаменатель остается 3. Итоговая неправильная дробь — \(\frac{8}{3}\).

Этот способ позволяет представить смешанное число в виде одной дроби, что упрощает сравнение и вычисления с другими дробями. Числитель 8 больше знаменателя 3, что указывает на то, что дробь больше единицы.

в) В смешанном числе \(3 \frac{1}{3}\) целая часть равна 3, дробная часть — \(\frac{1}{3}\). Для перевода в неправильную дробь умножаем целое число на знаменатель: \(3 \times 3 = 9\), затем прибавляем числитель: \(9 + 1 = 10\). Числитель новой дроби — 10, знаменатель остается 3. Получаем \(\frac{10}{3}\).

Это выражение показывает, что значение больше трёх единиц, что соответствует исходному смешанному числу. Неправильная дробь удобна для проведения арифметических операций, так как она не требует отдельного учета целой части.

г) Для смешанного числа \(2 \frac{5}{6}\) целая часть равна 2, дробная часть — \(\frac{5}{6}\). Преобразуем в неправильную дробь: умножаем целое число на знаменатель дроби: \(2 \times 6 = 12\), затем прибавляем числитель: \(12 + 5 = 17\). Числитель — 17, знаменатель — 6. Итог — \(\frac{17}{6}\).

Такое представление позволяет работать с числом как с единой дробью, что упрощает вычисления и сравнение. Числитель 17 больше знаменателя 6, что отражает значение, превышающее 2 целых.