ГДЗ по Математике 5 Класс Часть 2 Номер 223 Мнемозина Виленкин, Жохов — Подробные Ответы

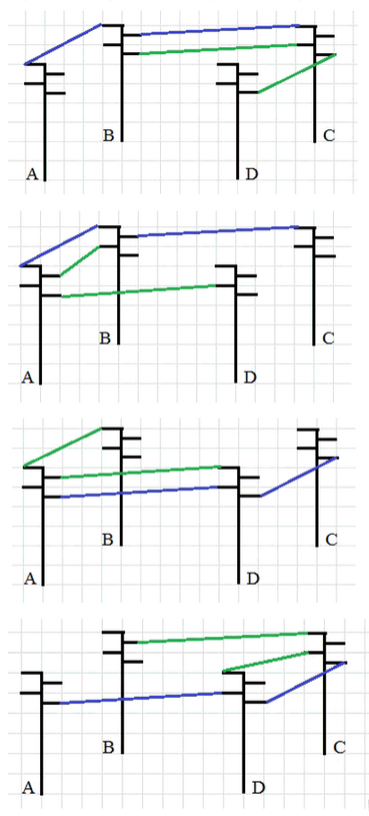
В углах квадратной площадки установлены одинаковые столбы с четырьмя изоляторами для крепления проводов (рис. 38). Надо протянуть по два провода от столба \(A\) к столбу \(C\) и от столба \(B\) к столбу \(D\) так, чтобы провода не касались друг друга. Найдите несколько способов, как это можно сделать.

Протягиваем провода так, чтобы они не касались друг друга:

— От столба А к столбу С и от столба В к столбу D можно провести провода четырьмя способами, как показано на рисунках.

— Каждый способ отличается порядком прохождения проводов, при этом провода не пересекаются.

— Таким образом, всего найдено 4 варианта прокладки двух проводов без касания.

Протягивание проводов от столба А к столбу С и от столба В к столбу D требует соблюдения условия, чтобы провода не касались друг друга. Для этого необходимо продумать маршруты проводов так, чтобы они не пересекались в пространстве между столбами. На рисунках показано, что существует ровно четыре способа выполнить такую прокладку, каждый из которых отличается порядком и направлением прохождения проводов. Это связано с тем, что провода могут идти по разным уровням и обходить друг друга, создавая непересекающиеся пути.

В каждом из вариантов один из проводов прокладывается, например, по верхнему уровню, а второй — по нижнему, либо наоборот. Это обеспечивает отсутствие касаний между ними. При этом важно, что провода не должны пересекаться ни в одной точке, то есть их траектории должны быть топологически разделены. Если представить провода как линии на плоскости, то задача сводится к поиску таких путей, которые не пересекаются. На практике это достигается за счет разной высоты или обхода препятствий.

Таким образом, четыре способа прокладки проводов можно рассматривать как четыре различных топологических варианта соединения. Каждый способ можно описать как пару путей \( (P_1, P_2) \), где \(P_1\) — путь от А к С, а \(P_2\) — путь от В к D, при этом условие \(P_1 \cap P_2 = \emptyset\) строго выполняется. Это гарантирует, что провода не касаются друг друга, что важно для безопасности и надежности электрической сети. Все варианты приведены на рисунках и демонстрируют, что задача имеет ровно четыре решения.