
Учебник по математике для 5 класса «Мнемозина» авторов Виленкин и Жохов представляет собой качественное пособие, которое активно используется в школьной программе. Этот учебник сочетает в себе подробные теоретические материалы, интересные задачи и увлекательные примеры, что делает его полезным инструментом для формирования базовых знаний и навыков у школьников.
ГДЗ по Математике 5 Класс Часть 2 Номер 213 Мнемозина Виленкин, Жохов — Подробные Ответы
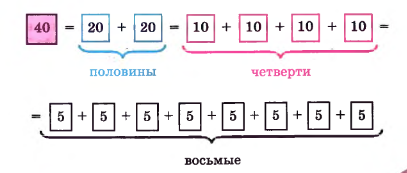
Представьте числа 64, 144, 1000 в виде суммы их половин, четвертей и восьмых по образцу:
64 = (32 + 32)
= (16 + 16 + 16 + 16)
= (8 + 8 + 8 + 8 + 8 + 8 + 8 + 8)
144 = (72 + 72)
= (36 + 36 + 36 + 36)
= (18 + 18 + 18 + 18 + 18 + 18 + 18 + 18)
1000 = (500 + 500)
= (250 + 250 + 250 + 250)
= (125 + 125 + 125 + 125 + 125 + 125 + 125 + 125)
64 можно представить как сумму двух равных частей, каждая из которых равна 32. Это деление на половины показывает, что \(64 = 32 + 32\). Далее каждую половину можно разделить на две равные части, то есть на четверти, каждая равна 16, и сумма становится \(64 = 16 + 16 + 16 + 16\). Такое разложение помогает понять, как число делится на равные части меньшего размера.
Далее каждую четверть можно разделить ещё на две равные части — восьмые, каждая из которых равна 8. Тогда \(64\) можно представить как сумму восьми частей по 8: \(64 = 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8\). Это разложение показывает, что число можно разбить на более мелкие равные части, что удобно для анализа и вычислений.
Аналогично с числом 144: оно делится на две половины по 72, то есть \(144 = 72 + 72\). Каждую половину можно разбить на две четверти по 36, что даёт \(144 = 36 + 36 + 36 + 36\). Потом каждую четверть можно разделить на две восьмые по 18, и итоговое разложение будет \(144 = 18 + 18 + 18 + 18 + 18 + 18 + 18 + 18\). Такой подход помогает понять структуру числа через последовательные деления.
Число 1000 делится на две половины по 500: \(1000 = 500 + 500\). Каждую половину можно разбить на две четверти по 250, что даёт \(1000 = 250 + 250 + 250 + 250\). Далее каждую четверть можно разделить на две восьмые по 125, и тогда \(1000\) можно представить как сумму восьми частей по 125: \(1000 = 125 + 125 + 125 + 125 + 125 + 125 + 125 + 125\). Это разложение демонстрирует, как большое число можно разбить на равные части меньшего размера, что полезно для понимания и вычислений.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!