ГДЗ по Математике 5 Класс Часть 2 Номер 212 Мнемозина Виленкин, Жохов — Подробные Ответы

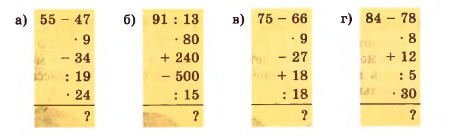
Вычислите устно:

а) \(55 — 47 = 8\);
\(8 \cdot 9 = 72\);
\(72 — 34 = 38\);
\(38 : 19 = 2\);
\(2 \cdot 24 = 48\).

б) \(91 : 13 = 7\);
\(7 \cdot 80 = 560\);
\(560 + 240 = 800\);
\(800 — 500 = 300\);
\(300 : 15 = 20\).

в) \(75 — 66 = 9\);
\(9 \cdot 9 = 81\);
\(81 — 27 = 54\);
\(54 + 18 = 72\);
\(72 : 18 = 4\).

г) \(84 — 78 = 6\);
\(6 \cdot 8 = 48\);
\(48 + 12 = 60\);
\(60 : 5 = 12\);
\(12 \cdot 30 = 360\).

а) Сначала вычисляем разность \(55 — 47\), так как вычитание — это базовая арифметическая операция, которая позволяет определить, насколько одно число меньше другого. Получаем \(8\). Далее умножаем результат на \(9\), то есть \(8 \cdot 9 = 72\). Умножение здесь служит для увеличения значения в 9 раз. Следующий шаг — вычесть из \(72\) число \(34\), что даёт \(38\). Это действие уменьшает значение, учитывая разницу между двумя величинами. Потом делим \(38\) на \(19\), получая \(2\). Деление показывает, сколько раз число \(19\) помещается в \(38\). В конце умножаем \(2\) на \(24\), что даёт \(48\), увеличивая число в 24 раза.

Таким образом, каждая операция логично связана с предыдущей, и последовательность действий демонстрирует, как изначальное число трансформируется через вычитание, умножение, вычитание, деление и снова умножение, что помогает понять взаимосвязь арифметических действий и их влияние на результат.

б) Начинаем с деления \(91 : 13\), чтобы определить, сколько раз число \(13\) умещается в \(91\), результат равен \(7\). Затем умножаем это число на \(80\), получая \(560\), что показывает масштабирование значения. После этого прибавляем \(240\) к \(560\), что даёт \(800\), увеличивая сумму на заданное число. Далее из \(800\) вычитаем \(500\), уменьшая результат до \(300\). В конце делим \(300\) на \(15\), получая \(20\), что показывает, сколько раз число \(15\) помещается в \(300\).

Каждое действие здесь последовательно меняет величину, показывая, как с помощью простых арифметических операций можно переходить от одного значения к другому, объясняя логику изменения чисел в процессе решения.

в) Сначала вычисляем разность \(75 — 66\), что даёт \(9\), показывая разницу между двумя числами. Потом умножаем \(9\) на \(9\), получая \(81\), что увеличивает число в 9 раз. Следующим шагом вычитаем из \(81\) число \(27\), получая \(54\), уменьшая величину. Затем прибавляем \(18\) к \(54\), что даёт \(72\), увеличивая сумму. В конце делим \(72\) на \(18\), получая \(4\), показывая, сколько раз число \(18\) содержится в \(72\).

Эта последовательность операций демонстрирует, как через вычитание, умножение, вычитание, сложение и деление можно последовательно изменять числа, что помогает понять взаимосвязь между арифметическими действиями.

г) Начинаем с вычитания \(84 — 78\), что даёт \(6\), показывая разницу между двумя числами. Умножаем \(6\) на \(8\), получая \(48\), увеличивая значение. Затем прибавляем \(12\) к \(48\), получая \(60\), что увеличивает сумму. Делим \(60\) на \(5\), получая \(12\), показывая, сколько раз число \(5\) помещается в \(60\). В конце умножаем \(12\) на \(30\), получая \(360\), что значительно увеличивает число.

Такой порядок действий показывает, как можно последовательно изменять значения с помощью базовых арифметических операций, каждая из которых влияет на конечный результат, демонстрируя логику и взаимосвязь между числами.